Γ Λυκείου / ΟΛΟΚΛΗΡΩΣΗ ΜΕ ΑΝΤΙΚΑΤΑΣΤΑΣΗ

ΟΛΟΚΛΗΡΩΣΗ ΑΡΡΗΤΗΣ ΣΥΝΑΡΤΗΣΗΣ

Σχολιάστε
Print Friendly, PDF & Email
Για την ολοκλήρωση άρρητης συναρτήσης, δηλαδή για ολοκληρώματα που περιέχουν ν-οστη ρίζα της μορφής:

    \[\int_{\alpha}^{\beta} f\Bigg(x,\sqrt[\nu]{g(x)}\Bigg) \,\, dx\]

Χρησιμοποιούμε τη μέθοδο της αντικατάστασης θέτοντας:

    \[\sqrt[\nu]{g(x)} = u \Rightarrow g(x)=u^{\nu} \quad (1.)\]

Οπότε έχουμε:

    \[g'(x)\, dx= \nu u^{\nu -1}\, du\]

Η μέθοδος την αντικατάστασης εφαρμόσιμη και έχει αξία όταν είναι εφικτή η επίλυση της εξίσωσης (1.)
ως προς x.

Παράδειγμα.1.

Να υπολογισθεί το ορισμένο ολοκλήρωμα:

    \[\int_{2}^{3}x^{2}\cdot \sqrt[3]{x-2}\, dx.\]

Λύση
Το ολοκλήρωμα προς επίλυση, είναι ορισμένο ολοκλήρωμα άρρητης συνάρτησης, αφου παρουσιάζεται ρίζα τρίτης τάξεως (3) \sqrt[3]{x-2}

    \[\int_{2}^{3}x^{2}\cdot \sqrt[3]{x-2}\, dx.\]

Θέτουμε \sqrt[3]{x-2}=u\Rightarrow x-2=u^{3}\Rightarrow x=u^{3}+2.
Οπότε:

    \begin{align*} &(x)' dx =(u^{3}+2)' du \Rightarrow\\ & dx =3u^{2} du. \end{align*}

Επιπλέον
για x= 2 και \sqrt[3]{x-2}=u\Rightarrow \sqrt[3]{2-2}=u\Rightarrow u= 0.
και
για x= 3 και \sqrt[3]{x-2}=u\Rightarrow \sqrt[3]{3-2}=u\Rightarrow u= 1.

Συνεπώς το αρχικό ολοκλήρωμα σύμφωνα με τις παραπάνω αντικαταστάσεις γίνεται:

    \begin{align*} & \int_{2}^{3}x^{2}\cdot \sqrt[3]{x-2}\, dx =\\\\ &\int_{0}^{1}(u^{3}+2)^{2}\cdot u \cdot 3u^{2} du=\\\\ &\int_{0}^{1}3\cdot (u^{6}+4u^{3}+4)\cdot u^{3} du=\\\\ &\int_{0}^{1}3\cdot (u^{9}+4u^{6}+4 u^{3}) du=\\\\ &\int_{0}^{1}3u^{9}+12u^{6}+12 u^{3} du. \end{align*}

Επειδή ισχύει \Bigg(\dfrac{u^{10}}{10}\Bigg)'=u^{9}, \Bigg(\dfrac{u^{7}}{7}\Bigg)'=u^{6} και \Bigg(\dfrac{u^{4}}{4}\Bigg)'=u^{3}, έχουμε:

    \begin{align*} &\int_{0}^{1}3u^{9}+12u^{6}+12 u^{3} du=\\\\ &\int_{0}^{1}3\cdot \Bigg(\dfrac{u^{10}}{10}\Bigg)'+12\cdot \Bigg(\dfrac{u^{7}}{7}\Bigg)' +12 \cdot \Bigg(\dfrac{u^{4}}{4}\Bigg)' du=\\\\ &\int_{0}^{1} \Bigg(3\cdot\dfrac{u^{10}}{10}+ 12\cdot\dfrac{u^{7}}{7} + 12 \cdot\dfrac{u^{4}}{4}\Bigg)' du=\\\\ &\int_{0}^{1} \Bigg(\dfrac{3}{10}\cdot u^{10}+ \dfrac{12}{7}\cdot u^{7} + 3\cdot u^{4}\Bigg)' du=\\\\ &\Bigg[\dfrac{3}{10}\cdot u^{10}+ \dfrac{12}{7}\cdot u^{7} + 3\cdot u^{4}\Bigg]_{0}^{1} =\\\\ &\Bigg(\dfrac{3}{10}\cdot 1^{10}+ \dfrac{12}{7}\cdot 1^{7} + 3\cdot 1^{4}\Bigg)-\Bigg(\dfrac{3}{10}\cdot 0+ \dfrac{12}{7}\cdot 0 + 3\cdot 0\Bigg)=\\\\ &\dfrac{3}{10}+ \dfrac{12}{7} + 3=\dfrac{351}{70}. \end{align*}

Παράδειγμα.2.

Να υπολογισθεί το ορισμένο ολοκλήρωμα:

    \[\int_{0}^{\sqrt[4]{3}}x^{7}\cdot \sqrt{x^{4}+1}\, dx.\]

Λύση
Το ολοκλήρωμα προς επίλυση, είναι ορισμένο ολοκλήρωμα άρρητης συνάρτησης, αφου παρουσιάζεται τετραγωνικη ρίζα \sqrt{x^{4}+1}

    \[\int_{0}^{\sqrt[4]{3}}x^{7}\cdot \sqrt{x^{4}+1}\, dx.\]

Θέτουμε \sqrt{x^{4}+1}=u\Rightarrow x^{4}+1=u^{2}\Rightarrow x^{4}=u^{2}-1.
Οπότε:

    \begin{align*} &(x^{4})'\, dx =(u^{2}-1)' \, du \Rightarrow\\ & 4x^{3} \,\,dx =2u\,\, du \Rightarrow\\ & 2x^{3} \,\,dx = u\,\, du \Rightarrow\\ & x^{3} \,\,dx = \dfrac{u}{2}\,\, du. \end{align*}

Επιπλέον
για x= 0 και \sqrt{x^{4}+1}=u\Rightarrow \sqrt{0^{4}+1}=u\Rightarrow u= 1.
και
για x= \sqrt[4]{3} και \sqrt{x^{4}+1}=u\Rightarrow \sqrt{\big(\sqrt[4]{3}\big)^{4}+1}=u\Rightarrow
\Rightarrow\sqrt{3+1}=u \Rightarrow\sqrt{4}=u \Rightarrow u = 2.

Συνεπώς το αρχικό ολοκλήρωμα σύμφωνα με τις παραπάνω αντικαταστάσεις γίνεται:

    \begin{align*} & \int_{0}^{\sqrt[4]{3}}x^{7}\cdot \sqrt{x^{4}+1}\, dx =\\\\ &\int_{0}^{\sqrt[4]{3}}x^{4}\cdot x^{3}\cdot \sqrt{x^{4}+1}\, dx =\\\\ &\int_{0}^{\sqrt[4]{3}}x^{4}\cdot \sqrt{x^{4}+1} \cdot x^{3}\, dx =\\\\ &\int_{1}^{2}(u^{2}-1)\cdot u \cdot \dfrac{u}{2}\, du =\\\\ &\int_{1}^{2}(u^{2}-1)\cdot \dfrac{u^{2}}{2}\, du =\\\\ &\int_{1}^{2} \dfrac{u^{4}-u^{2}}{2}\, du =\\\\ &\int_{1}^{2} \dfrac{1}{2}\cdot(u^{4}-u^{2})\, du =\\\\ \end{align*}

Επειδή ισχύει 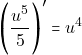\Bigg(\dfrac{u^{5}}{5}\Bigg)'=u^{4} και\Bigg(\dfrac{u^{3}}{3}\Bigg)'=u^{2} έχουμε:

    \begin{align*} &\int_{1}^{2} \dfrac{1}{2}\cdot(u^{4}-u^{2})\, du =\\\\ &\int_{1}^{2} \dfrac{1}{2}\cdot\Bigg[\bigg(\dfrac{u^{5}}{5}\bigg)'-\bigg(\dfrac{u^{3}}{3}\bigg)'\Bigg]\, du =\\\\ &\int_{1}^{2} \Bigg[\dfrac{1}{2}\cdot\bigg(\dfrac{u^{5}}{5}-\dfrac{u^{3}}{3}\bigg)\Bigg]'\, du =\\\\ &\Bigg[\dfrac{1}{2}\cdot\bigg(\dfrac{u^{5}}{5}-\dfrac{u^{3}}{3}\bigg)\Bigg]_{1}^{2}=\\\\ &\Bigg[\dfrac{1}{2}\cdot\bigg(\dfrac{1^{5}}{5}-\dfrac{1^{3}}{3}\bigg)\Bigg]-\Bigg[\dfrac{1}{2}\cdot\bigg(\dfrac{2^{5}}{5}-\dfrac{2^{3}}{3}\bigg)\Bigg]=...=\dfrac{29}{15} \end{align*}

Βιβλιογραφία: Παπαδακης, εκδόσεις Σαββάλα
Άδεια Creative Commons
Αυτή η εργασία χορηγείται με άδεια Creative Commons Αναφορά Δημιουργού – Μη Εμπορική Χρήση – Παρόμοια Διανομή 4.0 Διεθνές .

Αφήστε μια απάντηση

Η ηλ. διεύθυνση σας δεν δημοσιεύεται. Τα υποχρεωτικά πεδία σημειώνονται με *

Δεν είμαι Robot *