Γ Λυκείου / ΟΛΟΚΛΗΡΩΣΗ ΜΕ ΑΝΤΙΚΑΤΑΣΤΑΣΗ

ΟΛΟΚΛΗΡΩΜΑ ΣΥΝΑΡΤΗΣΗΣ ΜΕ ΡΙΖΕΣ ΔΙΑΦΟΡΕΤΙΚΗΣ ΤΑΞΗΣ ΜΕ ΙΔΙΟ ΥΠΟΡΡΙΖΟ

Σχολιάστε
Print Friendly, PDF & Email

Για να υπολογίσουμε το ορισμένο ολοκλήρωμα μιας συνάρτησης όπου ο τύπος της περιέχει ρίζες διαφορετικής τάξης οι οποίες όμως έχουν το ίδιο υπόρριζο, δηλαδή ολοκλήρώματα της μορφής:

    \[\int_{\alpha}^{\beta}f\big( x, \sqrt[\nu]{kx+\lambda}, \sqrt[\mu]{kx+\lambda}\big)\,\, dx, \quad k\in \rr^{*}\]

εργαζόμαστε ως εξης:

  • Βρίσκουμε το Ελάχιστο κοινό πολλαπλάσιο των τάξεων των ριζών π.χ. EK\Pi(\nu, \mu)=\gamma.
  • Θέτουμε \sqrt[\gamma]{kx+\lambda} =u\Rightarrow kx+\lambda = u^{\gamma}.
  • Οπότε ( kx+\lambda)' \, dx = ( u^{\gamma})' du \Rightarrow k\cdot dx = \gamma u^{\gamma -1} du.
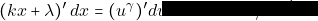
  • Γράφουμε τα ριζικά \sqrt[\nu]{kx+\lambda}, \sqrt[\mu]{kx+\lambda}, ως δυνάμεις του u και κάνουμε την αντικατάσταση.


    • Παράδειγμα.1.
    Να υπολογίσετε το οριμένο ολοκλήρωμα

        \[\int_{2}^{65} \dfrac{ \sqrt{x-1}+1}{\sqrt[3]{x-1}+\sqrt{x-1}}\, dx.\]


    Λύση
    Στο ολοκλήρωμα:

        \[\int_{2}^{65} \dfrac{ \sqrt{x-1}+1}{\sqrt[3]{x-1}+\sqrt{x-1}}\, dx.\]

    Υπάρχουν οι παρακάτω ρίζες διαφορετικής τάξης 2 και 3

        \[\sqrt{x-1}}, \quad \sqrt[3]{x-1}.\]

    Υπολογίζουμε το ελάχιστο κοινό πολλαπλάσιο των τάξεων EK\Pi(2,3)=6.

    Θέτουμε \sqrt[6]{x-1}=u\Rightarrow x-1=u^{6}.
    Οπότε:

        \begin{align*} &(x-1)'\, dx =(u^{6})' \, du \Rightarrow\\ & dx =6u^{5}\,\, du. \end{align*}

    Επιπλέον ισχύουν:

        \[\sqrt{x-1}=\sqrt[6]{x-1}^{3} =u^{3}\]

    και

        \[\sqrt[3]{x-1}=\sqrt[6]{x-1}^{2} =u^{2}\]

    για x= 2 και \sqrt[6]{x-1}=u\Rightarrow \sqrt[6]{2-1}=u\Rightarrow u= 1.
    και
    για x= 65 και \sqrt[6]{x-1}=u\Rightarrow \sqrt[6]{65-1}=u\Rightarrow \sqrt[6]{64}=u\Rightarrow \sqrt[6]{2^{6}}=u\Rightarrow u = 2

    Συνεπώς το αρχικό ολοκλήρωμα σύμφωνα με τις παραπάνω αντικαταστάσεις γίνεται:

        \begin{align*} &\int_{2}^{65} \dfrac{ \sqrt{x-1}+1}{\sqrt[3]{x-1}+\sqrt{x-1}}\, dx=\\\\ &\int_{1}^{2} \dfrac{ u^{3}+1}{u^{2}+u^{3}}\cdot 6u^{5}\,\, du=\\\\ &\int_{1}^{2} \dfrac{ u^{3}+1}{u^{2}\cdot (1+u)}\cdot 6u^{5}\,\, du=\\\\ &\int_{1}^{2} 6u^{3}\cdot \dfrac{ u^{3}+1}{(1+u)}\,\, du=\\\\ &\int_{1}^{2} 6u^{3}\cdot \dfrac{(u+1)\cdot( u^{2}-u+1)}{(1+u)}\,\, du=\\\\ &\int_{1}^{2} 6u^{3}\cdot ( u^{2}-u+1)\,\, du=\\\\ &\int_{1}^{2} 6u^{5}-6u^{4}+6u^{3}\,\, du=\\\\ \end{align*}

    Επειδή ισχύει \Bigg(\dfrac{u^{6}}{6}\Bigg)'=u^{5}, \, \Bigg(\dfrac{u^{5}}{5}\Bigg)'=u^{4} και \Bigg(\dfrac{u^{4}}{4}\Bigg)'=u^{3} έχουμε:

        \begin{align*} &\int_{1}^{2} 6u^{5}-6u^{4}+6u^{3}\,\, du=\\\\ &\int_{1}^{2} 6\cdot \Bigg(\dfrac{u^{6}}{6}\Bigg)'-6 \cdot \Bigg(\dfrac{u^{5}}{5}\Bigg)'+6\cdot \Bigg(\dfrac{u^{4}}{4}\Bigg)'\,\, du=\\\\ &\int_{1}^{2} \Bigg( 6\cdot \dfrac{u^{6}}{6}-6 \cdot \dfrac{u^{5}}{5}+6\cdot \dfrac{u^{4}}{4}\Bigg)'\,\, du=\\\\ &\int_{1}^{2} \Bigg(u^{6}- \dfrac{6}{5} \cdot u^{5}+\dfrac{3}{2}\cdot u^{4}\Bigg)'\,\, du=\\\\ &\Bigg[u^{6}- \dfrac{6}{5} \cdot u^{5}+\dfrac{3}{2}\cdot u^{4}\Bigg]_{1}^{2} =\\\\ &\Bigg[2^{6}- \dfrac{6}{5} \cdot 2^{5}+\dfrac{3}{2}\cdot 2^{4}\Bigg]- \Bigg[1^{6}- \dfrac{6}{5} \cdot 1^{5}+\dfrac{3}{2}\cdot 1^{4}\Bigg]=...=\dfrac{483}{10}.\\\\ \end{align*}

    Βιβλιογραφία: Παπαδακης, εκδόσεις Σαββάλα
    Άδεια Creative Commons
    Αυτή η εργασία χορηγείται με άδεια Creative Commons Αναφορά Δημιουργού – Μη Εμπορική Χρήση – Παρόμοια Διανομή 4.0 Διεθνές .

    Αφήστε μια απάντηση

    Η ηλ. διεύθυνση σας δεν δημοσιεύεται. Τα υποχρεωτικά πεδία σημειώνονται με *

    Δεν είμαι Robot *