ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ 1518 ΑΝΙΣΩΣΕΙΣ ΔΕΥΤΕΡΟΥ ΒΑΘΜΟΥ
ΑΛΓΕΒΡΑ Α ΛΥΚΕΙΟΥ
ΕΠΙΠΕΔΟ ΔΥΣΚΟΛΙΑΣ ΘΕΜΑΤΟΣ 4 ΤΕΤΑΡΤΟΥ
Για να μελετήσετε την παρούσα άσκηση θα πρέπει να γνωρίζετε την αντίστοιχη θεωρία η οποία βρίσκεται στους παρακάτω συνδέσμους:
4.1 Ανισώσεις πρώτου βαθμού,
4.2 Ανισώσεις δευτέρου βαθμού.

Λύση
1.) Είναι:
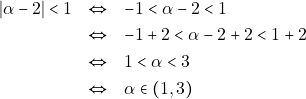
2.)
2a.) Το τριώνυμο ![]() έχει διακρίνουσα:
έχει διακρίνουσα:
![Rendered by QuickLaTeX.com \begin{eqnarray*} \Delta &=& \beta^2 - 4 \alpha\gamma \\\\ &=& \big[(-(\alpha - 2))\big]^2 - 4 \cdot 1 \cdot \dfrac{1}{4} \\\\ &=& \alpha^2 - 4\alpha + 4 - 1 \\\\ &=& \alpha^2 - 4\alpha + 3 \end{eqnarray*}](https://study4maths.gr/wp-content/ql-cache/quicklatex.com-0a56476ebbea508d3827ae9a4e839e46_l3.png)
Το τριώνυμο ![]() έχει διακρίνουσα:
έχει διακρίνουσα:
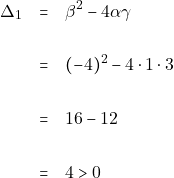
και ρίζες τις:
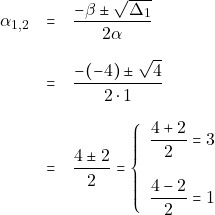
Το πρόσημο του τριωνύμου φαίνεται στον παρακάτω πίνακα.
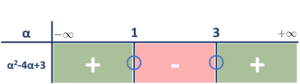

Από τον πίνακα προσήμων συμπεραίνουμε ότι: ![]()
2b.) Αφού το ![]() έχει
έχει ![]() θα έχει πρόσημο το ίδιο με το πρόσημο του συντελεστή του
θα έχει πρόσημο το ίδιο με το πρόσημο του συντελεστή του ![]() δηλαδή του
δηλαδή του ![]() Άρα:
Άρα:
![]()
Σχόλιο
Το σκέλος (2b.) μπορεί να λυθεί και ως εξής: Επειδή,
![Rendered by QuickLaTeX.com \begin{eqnarray*} \Delta &=& \big[-(\alpha - 2)\big]^2 - 4 \cdot 1 \cdot \dfrac{1}{4} \\\\ &=& (\alpha - 2)^2 - 1 \end{eqnarray*}](https://study4maths.gr/wp-content/ql-cache/quicklatex.com-1817273c657289724d166410ddfc793d_l3.png)
ισχύει ότι:
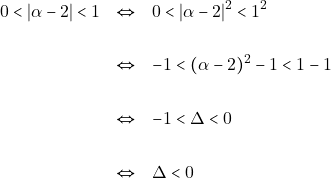
Βιβλιογραφία
http://iep.edu.gr/el/trapeza-thematon-arxiki-selida

Αυτή η εργασία χορηγείται με άδεια Creative Commons Αναφορά Δημιουργού – Μη Εμπορική Χρήση – Παρόμοια Διανομή 4.0 Διεθνές .
