ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ 1480 ΑΝΙΣΩΣΕΙΣ ΔΕΥΤΕΡΟΥ ΒΑΘΜΟΥ

ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ 1480 ΑΝΙΣΩΣΕΙΣ ΔΕΥΤΕΡΟΥ ΒΑΘΜΟΥ
ΑΛΓΕΒΡΑ Α ΛΥΚΕΙΟΥ
ΕΠΙΠΕΔΟ ΔΥΣΚΟΛΙΑΣ ΘΕΜΑΤΟΣ 4 ΤΕΤΑΡΤΟΥ
Για να μελετήσετε την παρούσα άσκηση θα πρέπει να γνωρίζετε την αντίστοιχη θεωρία η οποία βρίσκεται στους παρακάτω συνδέσμους:

3.3 Εξισώσεις δευτέρου βαθμού
4.2 Ανισώσεις δευτέρου βαθμού.

Rendered by QuickLaTeX.com

Λύση

1.) Το τριώνυμο $x^2 - 3x + 2$ έχει $\alpha = 1, ~\beta = -3, ~\gamma = 2$ και διακρίνουσα:

$\begin{eqnarray*} \Delta &=& \beta^2 - 4\alpha\gamma \\ &=& (-3)^2 - 4 \cdot 1 \cdot 2 \\ &=& 9 - 8 \\ &=& 1 > 0 \end{eqnarray*}$

Οι ρίζες της εξίσωσης είναι:

$\begin{eqnarray*} x_{1, 2} &=& \dfrac{-\beta \pm \sqrt{\Delta}}{2\alpha} \\ &=& \dfrac{-(-3) \pm \sqrt{1}}{2 \cdot 1} \\ &=& \dfrac{3 \pm 1}{2} = \left\{\begin{array}{ll} \dfrac{3 + 1}{2} = 2 \\[5mm] \dfrac{3 - 1}{2} = 1 \end{array}\right. \end{eqnarray*}$

2.) Θέτουμε στη δοθείσα εξίσωση $x^2 = y ~(3).$ Τότε:

$\begin{eqnarray*} x^4 - 3x^2 + 2 = 0 &\Leftrightarrow& (x^2)^2 - 3x^2 + 2 = 0 \\ &\Leftrightarrow& y^2 - 3y + 2 = 0 \end{eqnarray*}$

Η εξίσωση που προέκυψε είναι ίδια με το σκέλος (α’) οπότε έχει ρίζες τις $y_1 = 1, y_2 = 2.$

Για $y = 1$ η σχέση $(3)$ δίνει: $x^2 = 1 \Leftrightarrow (x = -1$ ή $x = 1).$

Για $y = 2$ η σχέση $(3)$ δίνει: $x^2 = 2 \Leftrightarrow (x = -\sqrt{2}$ ή $x = \sqrt{2}).$

2.) Επειδή το ζητούμενο τριώνυμο έχει $\alpha = 1 > 0$ το πρόσημο του θα είναι αυτό που δίνεται στον πίνακα που ακολουθεί.

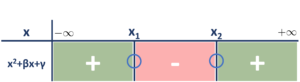
Πίνακας προσήμου τριωνύμου. — $x^{2}+\beta x+ \gamma.$

όπου $x_1, x_2$ οι ρίζες του με $x_1 < x_2$ και $x_1, x_2 \in \{-\sqrt{2}, -1, 1, \sqrt{2}\}.$

Για να είναι $x^2 + \beta x + \gamma > 0$ για κάθε $x < 0$ πρέπει οι ρίζες του $x_1, x_2$ να είναι θετικές αφού είναι $0 < x_1 < x_2.$

Διακρίνουμε τις περιπτώσεις:

$\color{red}1^{\text{η}}$ περίπτωση
Οι ρίζες να είναι $x_1 = 1$ και $x_2 = \sqrt{2}.$ Τότε από τους τύπους Vieta βρίσκουμε:
$S = x_1 + x_2 = 1 + \sqrt{2}$ και
$P = x_1 \cdot x_2 = 1 \cdot \sqrt{2} = \sqrt{2}$
Το ζητούμενο τριώνυμο είναι το:

$\begin{eqnarray*} &x^2 - Sx + P = x^2 - (1 + \sqrt{2})x + \sqrt{2} \end{eqnarray*}$

$\color{red}2^{\text{η}}$ περίπτωση
Οι ρίζες να είναι $x_1 = 1$ και $x_2 = 1.$ Τότε από τους τύπους Vieta βρίσκουμε:
$S = x_1 + x_2 = 1 + 1 = 2$ και
$P = x_1 \cdot x_2 = 1 \cdot 1 = 1$
Το ζητούμενο τριώνυμο είναι το: