ΕΣΩΤΕΡΙΚΟ ΓΙΝΟΜΕΝΟ ΔΙΑΝΥΣΜΑΤΩΝ ΑΠΟ ΓΡΑΜΜΙΚΟ ΣΥΝΔΥΑΣΜΟ

Σχέση της μορφής $\boldsymbol{\kappa \vec{α} + \lambda \vec{\beta} + \mu \vec{\gamma} = \vec{0}}$

Αν για τα διανύσματα $\vec{α}, \vec{\beta}$ και $\vec{\gamma}$ ισχύει μια σχέση της μορφής:

$\kappa \vec{α} + \lambda \vec{\beta} + \mu \vec{\gamma} = \vec{0}\quad \text{ με}\quad \kappa, \lambda, \mu \in \mathbb{R}$

και γνωρίζουμε τα $\lvert \vec{α} \rvert, \lvert \vec{\beta} \rvert$ και $\lvert \vec{\gamma} \rvert,$ τότε μπορούμε να υπολογίζουμε καθένα από τα εσωτερικά γινόμενα $\vec{α} \cdot \vec{\beta}, ~\vec{\beta} \cdot \vec{\gamma}$ και $\vec{\gamma} \cdot \vec{α}.$

Για παράδειγμα, μπορούμε να υπολογίσουμε το

$\vec{α} \cdot \vec{\beta}$

ως εξής:

$\kappa \vec{α} + \lambda \vec{\beta} + \mu \vec{\gamma} = \vec{0} \Leftrightarrow$

$\kappa \vec{α} + \lambda \vec{\beta} = -\mu \vec{\gamma}$

άρα:

$(\kappa \vec{α} + \lambda \vec{\beta})^{2} = (-\mu \vec{\gamma})^{2} \Leftrightarrow$

$\kappa^{2} \vec{α}^{2} + 2\cdot\kappa \cdot\lambda\cdot \vec{α} \cdot \vec{\beta} + \lambda^{2} \vec{\beta}^{2} = \mu^{2} \vec{\gamma}^{2} \Leftrightarrow$

$\kappa^{2} \lvert \vec{α} \rvert^{2} + 2\cdot\kappa \cdot\lambda \cdot\vec{α} \cdot \vec{\beta} + \lambda^2 \lvert \vec{\beta} \rvert^{2} = \mu^{2} \lvert \vec{\gamma} \rvert^{2} \Leftrightarrow \dots$

Rendered by QuickLaTeX.com

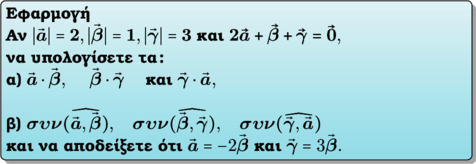
ΛΥΣΗ

α) Έχουμε:

$2\vec{α} + \vec{\beta} + \vec{\gamma} = \vec{0} \Leftrightarrow 2\vec{α} + \vec{\beta} = - \vec{\gamma}$

άρα:

$(2 \vec{\alpha}+\vec{\beta})^{2} = (-\vec{\gamma})^{2} \Leftrightarrow$

$4 \vec{a}^{2}+4 \vec{\alpha} \cdot \vec{\beta}+\vec{\beta}^{2}=\vec{\gamma}^{2} \xLeftrightarrow [\vec{\gamma}^{2}=|\vec{\gamma}|^{2}]{\vec{a}^{2} = |\vec{a}|^{2}\quad \vec{\beta}^{2}=|\vec{\beta}|^{2}}$

$4 \lvert \vec{\alpha}|^{2}+4 \vec{\alpha} \cdot \vec{\beta}+|\vec{\beta}\rvert^{2}=|\vec{\gamma}|^{2} \Leftrightarrow$

$4 \cdot 2^{2}+4 \vec{\alpha} \cdot \vec{\beta}+1^{2} = 3^{2} \Leftrightarrow$

$4 \vec{\alpha} \cdot \vec{\beta} = -8 \Leftrightarrow$

$\vec{\alpha} \cdot \vec{\beta} = -2$

Ομοίως είναι

$2\vec{α} + \vec{\beta} + \vec{\gamma} = \vec{0} \Leftrightarrow \vec{\beta}+ \vec{\gamma} = - 2 \vec{α},$

άρα:

$(\vec{\beta}+\vec{\gamma})^{2} = (-2 \vec{\alpha})^{2} \Leftrightarrow$

$\vec{\beta}^{2}+2 \vec{\beta} \cdot \vec{\gamma}+\vec{\gamma}^{2} = 4 \vec{\alpha}^{2} \xLeftrightarrow [\vec{\gamma}^{2}=|\vec{\gamma}|^{2}]{\vec{a}^{2} = |\vec{a}|^{2}\quad \vec{\beta}^{2}=|\vec{\beta}|^{2}}$

$\lvert \vec{\beta}\rvert^{2}+2 \vec{\beta} \cdot \vec{\gamma}+\lvert\vec{\gamma}\rvert^{2} = 4\lvert\vec{\alpha}\rvert^{2} \Leftrightarrow$

$1 + 2 \vec{\beta} \cdot \vec{\gamma}+9=16 \Leftrightarrow$

$\vec{\beta} \cdot \vec{\gamma} = 3$

Τέλος είναι

$2\vec{α} + \vec{\beta} + \vec{\gamma} = \vec{0} \Leftrightarrow2\vec{α} + \vec{\gamma} = - \vec{\beta},$

άρα:

$(2 \vec{\alpha}+\vec{\gamma})^{2} = (-\vec{\beta})^{2} \Leftrightarrow$

$4 \vec{\alpha}^{2} + 4 \vec{\alpha} \cdot \vec{\gamma} + \vec{\gamma}^{2} = \vec{\beta}^{2} \xLeftrightarrow [\vec{\gamma}^{2}=|\vec{\gamma}|^{2}]{\vec{a}^{2} = |\vec{a}|^{2}\quad \vec{\beta}^{2}=|\vec{\beta}|^{2}}$

$4\lvert \vec{\alpha}\rvert^{2} + 4 \vec{\gamma} \cdot \vec{\alpha} + \lvert \vec{\gamma}\rvert^{2 } = \lvert \vec{\beta} \rvert^{2} \Leftrightarrow$

$16 + 4 \vec{\gamma} \cdot \vec{\alpha}+9 = 1 \Leftrightarrow$

$\vec{\gamma} \cdot \vec{a} = -6$

β)
Έχουμε:

$\begin{align*} &\sigma \upsilon \nu(\widehat{\vec{α}, \vec{\beta}}) = \frac{\vec{α} \cdot \vec{\beta}}{\lvert \vec{α} \rvert \lvert \vec{\beta} \rvert} = \frac{-2}{2 \cdot 1} = -1\\\\ &\sigma \upsilon \nu(\widehat{\vec{\beta}, \vec{\gamma}}) = \frac{\vec{\beta} \cdot \vec{\gamma}}{\lvert \vec{\beta} \rvert \lvert \vec{\gamma} \rvert} = \frac{3}{1 \cdot 3} = 1\\\\ &\sigma \upsilon \nu(\widehat{\vec{\gamma}, \vec{α}}) = \frac{\vec{\gamma} \cdot \vec{α}}{\lvert \vec{\gamma} \rvert \lvert \vec{α} \rvert} = \frac{-6}{3 \cdot 2} = -1 \end{align*}$

Είναι $\sigma \upsilon \nu(\widehat{\vec{α}, \vec{\beta}})=-1,$ άρα $\vec{α} \uparrow \downarrow \vec{\beta}$ και επειδή $\lvert \vec{α} \rvert = 2 \lvert \vec{\beta} \rvert,$ ισχύει ότι $\vec{α} = -2\vec{\beta}.$

Ομοίως είναι $\sigma \upsilon \nu(\widehat{\vec{\beta}, \vec{\gamma}}) = 1,$ άρα $\vec{\beta} \uparrow \uparrow \vec{\gamma}$ και επειδή $\lvert \vec{\gamma} \rvert = 3 \lvert \vec{\beta} \rvert,$ ισχύει ότι $\vec{\gamma} = 3\vec{\beta}.$

Βιβλιογραφία:
Παπαδάκης εκδόσεις Σαββάλα.

Αυτή η εργασία χορηγείται με άδεια Creative Commons Αναφορά Δημιουργού – Μη Εμπορική Χρήση – Παρόμοια Διανομή 4.0 Διεθνές .

Δ	Τ	Τ	Π	Π	Σ	Κ
1	2	3	4	5	6	7
8	9	10	11	12	13	14
15	16	17	18	19	20	21
22	23	24	25	26	27	28
29	30

Ν. Α. Διακόπουλος

ΕΣΩΤΕΡΙΚΟ ΓΙΝΟΜΕΝΟ ΔΙΑΝΥΣΜΑΤΩΝ ΑΠΟ ΓΡΑΜΜΙΚΟ ΣΥΝΔΥΑΣΜΟ

Αφήστε μια απάντηση Ακύρωση απάντησης

Ένας ιστότοπος για τα Μαθηματικά