Παράδειγμα.
Δίνεται η συνάρτηση ![]() Να αποδείξετε ότι η γραφική παράσταση της συνάρτησης,
Να αποδείξετε ότι η γραφική παράσταση της συνάρτησης, ![]() έχει οριζόντια ασύμπτωτη στο
έχει οριζόντια ασύμπτωτη στο ![]() και ότι η γραφική παράσταση
και ότι η γραφική παράσταση ![]() τέμνει τη παραπάνω ασύμπτωτη σε άπειρα σημεία.
τέμνει τη παραπάνω ασύμπτωτη σε άπειρα σημεία.
Λύση
Η συνάρτηση
![]()
ορίζεταιστο ![]() Έχουμε:
Έχουμε:
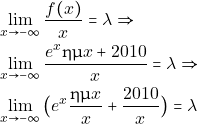
Υπολόγισμός του ορίου:![]()
Ισχύει ότι:
![]()
Άρα
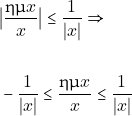
Επίσης έχουμε ότι:
![]()
Σύμφωνα με το κριτήριο παρεμβολής ισχύει ότι
![]()
Επομένως είναι:
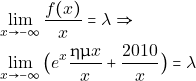
Άρα ![]() επομένως η γραφική παράσταση της
επομένως η γραφική παράσταση της ![]() θα έχει στο
θα έχει στο ![]() οριζόντια ασύμπτωτη.
οριζόντια ασύμπτωτη.
Οπότε
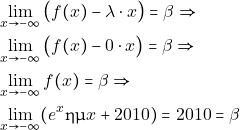
Άφου, για το όριο, ![]() έχουμε ότι
έχουμε ότι
![]()
Άρα
![]()
δηλαδη
![]()
Με ![]()
οπότε απο κριτήριο παρεμβολής ![]()
Επομένως, η ευθεία ![]() είναι οριζόντια ασύμπτωτη της
είναι οριζόντια ασύμπτωτη της ![]() στο
στο ![]()
Για να βρούμε τα σημεία τομής της ![]() και της
και της ![]() λύνουμε το σύστημα:
λύνουμε το σύστημα:
![]()
Απο το οποίο προκύπτει η εξίσωση:
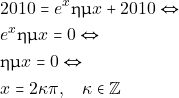
Δηλαδή η ![]() με
με ![]() τέμνει την ευθεια
τέμνει την ευθεια ![]() σε άπειρα σημεια της μορφής
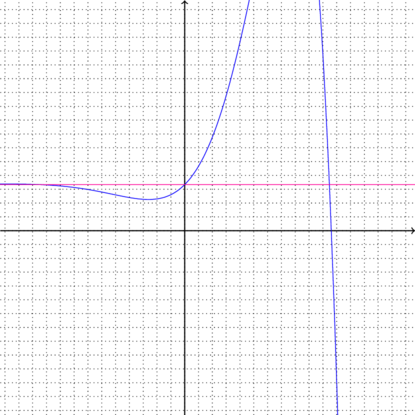
σε άπειρα σημεια της μορφής ![]() όπως διακρίνεται στο πρόχειρο σχήμα που ακολουθεί.
όπως διακρίνεται στο πρόχειρο σχήμα που ακολουθεί.
Βιβλιογραφία: Παπαδάκης, εκδόσεις Σαββάλα.

Αυτή η εργασία χορηγείται με άδεια Creative Commons Αναφορά Δημιουργού – Μη Εμπορική Χρήση – Παρόμοια Διανομή 4.0 Διεθνές .
