ΜΟΝΟΤΟΝΙΑ ΚΑΙ ΣΥΝΘΕΣΗ ΣΥΝΑΡΤΗΣΕΩΝ
Στις περιπτώσεις που ζητάμε την μονοτονία μιας συνάρτησης
![]()
Πρέπει να υπολογίσουμε την μονοτονία της ![]() της
της ![]() οπότε θα είναι γνωστή και η μονοτονία της σύνθεσης τών συναρτήσεων
οπότε θα είναι γνωστή και η μονοτονία της σύνθεσης τών συναρτήσεων ![]() με
με ![]() δηλαδη της
δηλαδη της ![]()
Παράδειγμα.
Να βρείτε την μονοτονία της συνάρτησης
![]()
Λύση
Από υπόθεση για κάθε ![]() ισχύει ότι:
ισχύει ότι:
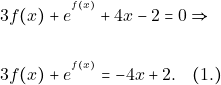
Το Α. μέλος της σχέσης(1.) γράφεται ως σύνθεση των συναρτήσεων ![]() και
και ![]() με
με ![]()
![]()
Υπολογίζουμε την μονοτονία της ![]()
Ισχύει: για ![]() με
με
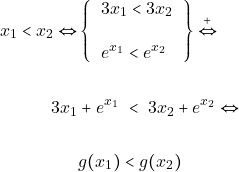
Άρα η συνάρτηση ![]() είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο ![]()
Ορίζουμε τώρα το Β. μέλος της σχέσης (1.)
ως συνάρτηση ![]() με
με ![]()
Υπολογίζουμε την μονοτονία της ![]() και έχουμε:
και έχουμε:
![]()
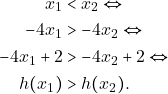
Άρα η συνάρτηση ![]() είναι γνησίως φθίνουσα στο
είναι γνησίως φθίνουσα στο ![]()
Συνοψίζοντας έχουμε ότι: από τις σχέσεις (1.) (2.) (3.)
![]()
Επειδη η ![]() είναι γνησίως φθίνουσα στο
είναι γνησίως φθίνουσα στο ![]() άρα και η
άρα και η ![]() είναι γνησίως φθίνουσα στο
είναι γνησίως φθίνουσα στο ![]()
οπότε για κάθε ![]() με
με
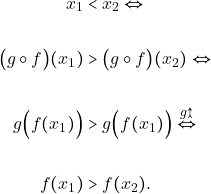
Δηλαδή η συνάρτηση ![]() είναι γνησίως φθίνουσα στο
είναι γνησίως φθίνουσα στο ![]()
ΝΑ ΛΥΘΟΥΝ ΟΙ ΠΑΡΑΚΑΤΩ ΑΣΚΗΣΕΙΣ
Έστω η συνάρτηση ![]() να βρεθει η μονοτονια της
να βρεθει η μονοτονια της ![]() στις παρακάτω περιπτωσεις
στις παρακάτω περιπτωσεις
i.) Αν ισχύει ![]() για κάθε
για κάθε ![]()
ii.) Αν ισχύει ![]() για κάθε
για κάθε ![]()
iii.) Αν ισχύει ![]() για κάθε
για κάθε ![]()
Βιβλιογραφία: Μπάρλας εκδόσεις Ελληνοεκδοτική.

Αυτή η εργασία χορηγείται με άδεια Creative Commons Αναφορά Δημιουργού – Μη Εμπορική Χρήση – Παρόμοια Διανομή 4.0 Διεθνές .
