ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ 1239 ΑΠΟΛΥΤΗ ΤΙΜΗ ΠΡΑΓΜΑΤΙΚΟΥ ΑΡΙΘΜΟΥ
ΑΛΓΕΒΡΑ Α ΛΥΚΕΙΟΥ
ΕΠΙΠΕΔΟ ΔΥΣΚΟΛΙΑΣ ΘΕΜΑΤΟΣ 2 ΔΕΥΤΕΡΟΥ
Για να μελετήσετε την παρούσα άσκηση θα πρέπει να γνωρίζετε την αντίστοιχη θεωρία η οποία βρίσκεται στους παρακάτω συνδέσμους:
2.2 Διάταξη πραγματικών αριθμών,
2.3 Απόλυτη τιμή πραγματικού αριθμού.
Λύση
1.)
1a) Ισχύει ότι:
![\[x \geq 2 \Leftrightarrow 3x \geq 3 \cdot 2 \Leftrightarrow 3x - 6 \geq 0\]](https://study4maths.gr/wp-content/ql-cache/quicklatex.com-19a867131ee560caf307e7f1497f79ae_l3.png "Rendered by QuickLaTeX.com")
Άρα 
Τότε:
![\[Α = |3x - 6| + 2 = 3x - 6 + 2 = 3x - 4\]](https://study4maths.gr/wp-content/ql-cache/quicklatex.com-1f5f7a3ce40a1a0b3462e18336494679_l3.png "Rendered by QuickLaTeX.com")
1b) Ισχύει ότι:
![\[x < 2 \Leftrightarrow 3x < 3 \cdot 2 \Leftrightarrow 3x - 6 < 0\]](https://study4maths.gr/wp-content/ql-cache/quicklatex.com-938710c34eafeac842f062837d33c91c_l3.png "Rendered by QuickLaTeX.com")
Άρα 
Τότε:
![\[A = |3x - 6| + 2 = 6 - 3x + 2 =8 - 3x\]](https://study4maths.gr/wp-content/ql-cache/quicklatex.com-f111c1aa47531ea8ee478a363ea0e034_l3.png "Rendered by QuickLaTeX.com")
2.) Για κάθε 
είναι 
Τότε:
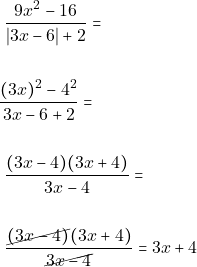
Βιβλιογραφία
http://iep.edu.gr/el/trapeza-thematon-arxiki-selida
Αυτή η εργασία χορηγείται με άδεια Creative Commons Αναφορά Δημιουργού – Μη Εμπορική Χρήση – Παρόμοια Διανομή 4.0 Διεθνές .