Γ Λυκείου,ΚΑΝΟΝΕΣ DE L' HOSPITAL

ΟΡΙΣΜΟΣ ΠΑΡΑΓΩΓΟΥ ΚΑΙ ΚΑΝΟΝΑΣ DE L HOSPITAL

Σχολιάστε
Print Friendly, PDF & Email


Παράδειγμα.1
Έστω f:\rr\to\rr μια συνάρτηση παραγωγίσιμη με f(0)=f'(0)=0, \, f''(0)=2.

Αν:

    \[ g(x)=\left\{ \begin{tabular}{ll} $\dfrac{f(x)}{x}, \quad x\neq 0$ \\\\ $ 0, \quad x=0$ \end{tabular} \right. \]

i_) Να βρείτε την g'(0).
ii_) Να δείξετε ότι η g' είναι συνεχής στο x_{0}=0.

Λύση

Έχουμε:

    \[g'(0)=\lim_{x\to 0}\dfrac{g(x)-g(0)}{x-0} =\lim_{x\to 0}\dfrac{\frac{f(x)}{x}-0}{x}=\lim_{x\to 0} \dfrac{f(x)}{x^{2}}. \quad (1)\]

Επειδή η συνάρτηση f είναι παραγωγίσιμη στο \rr οπότε είναι και συνεχής στο \rr άρα στο x_{0}=0, θα έχουμε:

    \[\lim_{x\to 0} f(x) =f(0)=0.\]

Συνεπώς

    \[\lim_{x\to 0}\dfrac{f(x)}{x^{2}}\xlongequal[D.L.H]{\frac{0}{0}}&\lim_{x\to 0}\dfrac{f'(x)}{2x}=\dfrac{0}{0}. \, (2)\]

Επειδή από υπόθεση f''(0)=0 αλλα η συνάρτηση f όχι δύο φορές παραγωγίσιμη, αρα για την παραπάνω απροσδιόριστη μορφή δεν μπορούμε να εφαρμόσουμε τον κανόνα του DEL HOSPITAL οπότε:

    \begin{align*} &\lim_{x\to 0}\dfrac{f'(x)}{2x}=\\\\ &\dfrac{1}{2}\lim_{x\to 0}\dfrac{f'(x)}{x}=\\\\ &\dfrac{1}{2}\lim_{x\to 0}\dfrac{f'(x)-0}{x-0}=\\\\ &\dfrac{1}{2}\lim_{x\to 0}\dfrac{f'(x)-f'(0)}{x-0}=\\\\ &\dfrac{1}{2}f''(0)=\dfrac{1}{2}\cdot 2 =1. \, (3) \end{align*}

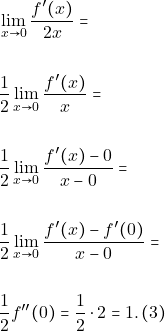
Τελικά απο τις σχέσεις (1) (2) (3) έχουμε ότι

    \[g'(0) =1.\]

ii-) Είναι

    \[ g(x)=\left\{ \begin{tabular}{ll} $\dfrac{x\cdot f'(x)- f(x)}{x^{2}}, \quad x\neq 0$ \\\\ $ 1, \quad x=0$ \end{tabular} \right. \]

Για να είναι η g’ συνεχής στο x_{0}=0 θα πρέπει \displaystyle\lim_{x\to 0}g'(x)=g'(0).
Έχουμε:

    \begin{align*} \lim_{x\to 0}g'(x) =& \lim_{x \to 0}\dfrac{x\cdot f'(x)- f(x)}{x^{2}}=\\\\ =& \lim_{x\to 0} \Bigg(\dfrac{x\cdot f'(x)}{x^{2}}-\dfrac{f(x)}{x^{2}}\Bigg)=\\\\ =& \lim_{x\to 0} \Bigg(\dfrac{ f'(x)}{x}-\dfrac{f(x)}{x^{2}}\Bigg)=\\\\ =& \lim_{x\to 0} \Bigg(\dfrac{ f'(x)-f'(0)}{x-0}-\dfrac{f(x)}{x^{2}}\Bigg)=\\\\ =& \lim_{x\to 0} \dfrac{ f'(x)-f'(0)}{x-0}-\lim_{x\to 0}\dfrac{f(x)}{x^{2}}=\\\\ =& f''(0)-1 =2-1=1=g'(0) \end{align*}

Άρα η g' είναι συνεχής στο x_{0}=0.

Βιβλιογραφία: Μπάρλας εκδόσεις Ελληνοεκδοτική.

Άδεια Creative Commons
Αυτή η εργασία χορηγείται με άδεια Creative Commons Αναφορά Δημιουργού – Μη Εμπορική Χρήση – Παρόμοια Διανομή 4.0 Διεθνές .

Αφήστε μια απάντηση

Η ηλ. διεύθυνση σας δεν δημοσιεύεται. Τα υποχρεωτικά πεδία σημειώνονται με *

Δεν είμαι Robot *