Έστω
![Rendered by QuickLaTeX.com \[\begin{cases} M\big(x_{0},f(x_{0})\big)\in (\epsilon):y =\lambda x+\beta\Leftrightarrow f(x_{0})=\lambda x_{0}+\beta\\\\ \quad \text{και} \\\\ f'(x_{0})=\lambda \end{cases}\]](https://study4maths.gr/wp-content/ql-cache/quicklatex.com-d9f45cedf8a0e5043d256c9057fbbc33_l3.png)
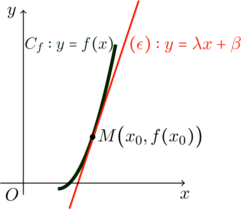
Παράδειγμα
Να δείξετε ότι η ευθεία ![]() εφάπτεται στη γραφική παράσταση της συνάρτησης
εφάπτεται στη γραφική παράσταση της συνάρτησης ![]() και να βρεθεί το σημείο επαφής.
και να βρεθεί το σημείο επαφής.
Λύση
Η συνάρτηση ![]() έχει πεδίο ορισμού το
έχει πεδίο ορισμού το ![]() με παράγωγο
με παράγωγο ![]() για κάθε
για κάθε ![]()
Για να είναι η ευθεία ![]() εφαπτομένη της γραφικής παράστασης, της συνάρτησης
εφαπτομένη της γραφικής παράστασης, της συνάρτησης ![]() με τύπο
με τύπο ![]() θα πρέπει να υπάρχει ένα
θα πρέπει να υπάρχει ένα ![]() τέτοιο ώστε το σημείο
τέτοιο ώστε το σημείο ![]() να είναι κοινο της γραφικής παράστασης της συνάρτησης
να είναι κοινο της γραφικής παράστασης της συνάρτησης ![]() και της ευθείας
και της ευθείας ![]() και επιπλέον η κλίση
και επιπλέον η κλίση ![]() της ευθείας
της ευθείας ![]() να είναι ίση με την παράγωγο της συνάρτησης
να είναι ίση με την παράγωγο της συνάρτησης ![]() στο
στο ![]() δηλαδή
δηλαδή ![]()
Δηλαδή
![Rendered by QuickLaTeX.com \begin{align*} &\begin{cases} M(x_{0},y_{0})\in C_{f}\\\\ \text{και}\\\\ M(x_{0},y_{0})\in (\epsilon):y = 3x-2\\\\ \text{και}\\\\ f'(x_{0})= \lambda_{(\epsilon)} \end{cases} \Leftrightarrow \\\\ &\begin{cases} y_{0}=f(x_{0}),\,\,(3)\\\\ \text{και}\\\\ y_{0} = 3x_{0}-2\\\\ \text{και}\\\\ f'(x_{0})= 3 \end{cases} \xLeftrightarrow{(3)} \\\\ &\begin{cases} f(x_{0}) = 3x_{0}-2\\\\ \text{και}\\\\ f'(x_{0})= 3 \end{cases} \xLeftrightarrow[(2)]{(1)} \\\\ &\begin{cases} x_{0}^{2}+x_{0}-1 = 3x_{0}-2\\\\ \text{και}\\\\ 2x_{0}+1= 3 \end{cases} \end{align*}](https://study4maths.gr/wp-content/ql-cache/quicklatex.com-d1f9ddd99f7909ab822cbb7e3fdadc0a_l3.png)
Από το παραπάνω σύστημα βρίσκουμε την τιμή του ![]()
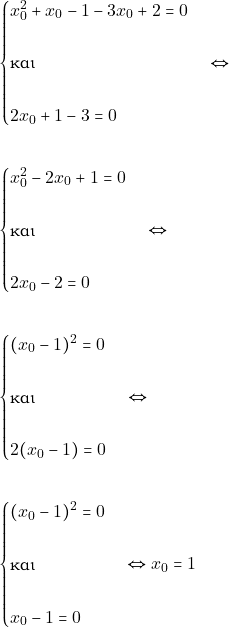
Άρα για ![]() έχουμε ότι
έχουμε ότι ![]()
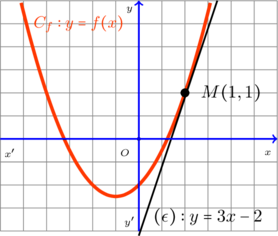
Τελικά η ευθεία ![]() εφάπτεται στη γραφική παράσταση της συνάρτησης
εφάπτεται στη γραφική παράσταση της συνάρτησης ![]() στο σημείο
στο σημείο ![]()
Βιβλιογραφία: Μπάρλας εκδόσεις Μπάρλας.

Αυτή η εργασία χορηγείται με άδεια Creative Commons Αναφορά Δημιουργού – Μη Εμπορική Χρήση – Παρόμοια Διανομή 4.0 Διεθνές .
