ΣΥΝΑΡΤΗΣΗ ΟΧΙ 1-1

ΣΥΝΑΡΤΗΣΗ ΟΧΙ 1-1

Συνήθως, οι συναρτήσεις που περιέχουν στον αλγεβρικό τους τύπο, $x^{2}, \,\, \syn x, \,\, \hm x$ ή απολυτες τιμες του $x$ δεν είναι συναρτήσεις ένα προς ένα $1-1.$ Σε αυτές τις περιπτωσεις προσπαθούμε να βρούμε κατάλληλο αντιπαράδειγμα ώστε να μην ισχύει ο ορισμός

$x_{1}\neq x_{2}\Rightarrow f(x_{1})\neq f(x_{2}).$

Rendered by QuickLaTeX.com

Λύση

ΣΥΝΑΡΤΗΣΗ ΟΧΙ 1-1

Παρατηρούμε ότι $f(0) =f(1)=1$ άρα η $f$ όχι $1-1.$
Παρατηρούμε ότι $f(0) =f(1)=0$ άρα η $f$ όχι $1-1.$
Η $f(x) =\sigma\upsilon\nu x +x\eta\mu x.$ έχει πεδίο ορισμού $A_{f}=\mathbb{R.}$
οπότε για κάθε $x\in A_{f}$ και $-x \in A_{f}.$
επίσης

$\begin{align*} f(-x)=& \sigma\upsilon\nu(- x) +(-x)\cdot\eta\mu (-x)\\ =& \sigma\upsilon\nu x +(-x)\cdot\big(-\eta\mu x\big)\\ =& \sigma\upsilon\nu x +x\cdot\eta\mu x\\ =& f(x). \end{align*}$

Άρα η $f$ είναι άρτια επομένως δεν είναι 1-1.
Για να βρούμε κατάλληλες τιμές για τα $x_{1}, \, x_{2}$ επιλέγουμε μια τυχαία τιμή για να εξισώσουμε το $|x-1|$ π.χ. το 2
έχουμε: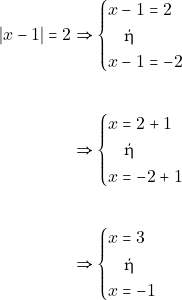

$\begin{align*} |x-1|=2 &\Rightarrow \begin{cases} x-1 =2 \\ \quad \text{ή} \\ x-1 =-2 \end{cases}\\\\ &\Rightarrow \begin{cases} x=2+1 \\ \quad \text{ή} \\ x =-2 +1\end{cases}\\\\ &\Rightarrow \begin{cases} x=3 \\ \quad \text{ή} \\ x =-1\end{cases} \end{align*}$

Οπότε η $f(x) = |x-1|-3$
για $x_{1} = 3$ δίνει:

$f(3)=|3-1|-3\Rightarrow f(3)= 2-3\Rightarrow f(3)=-1$

και για $x_{2}=-1$ έχουμε:

$f(-1)=|-1-1|-3\Rightarrow f(-1)= |-2|-3\Rightarrow$

$f(-1)=2-3 \Rightarrow f(-1)=-1.$

δηλαδή: $f(3)= f(-1)$ άρα η $f$ όχι $1-1.$

Βιβλιογραφία: Παπαδάκης, εκδόσεις Σαββάλα. Δ.Α.Παπακωνσταντίνου, αυτοέκδοση.

Αυτή η εργασία χορηγείται με άδεια Creative Commons Αναφορά Δημιουργού – Μη Εμπορική Χρήση – Παρόμοια Διανομή 4.0 Διεθνές .

Δ	Τ	Τ	Π	Π	Σ	Κ
			1	2	3	4
5	6	7	8	9	10	11
12	13	14	15	16	17	18
19	20	21	22	23	24	25
26	27	28	29	30	31

Ν. Α. Διακόπουλος

ΣΥΝΑΡΤΗΣΗ ΟΧΙ 1-1

Αφήστε μια απάντηση Ακύρωση απάντησης

Ένας ιστότοπος για τα Μαθηματικά