ΑΣΚΗΣΕΙΣ ΕΣΩΤΕΡΙΚΟΥ ΓΙΝΟΜΕΝΟΥ ΜΕΡΟΣ Γ.
-
- Αν
 να αποδείξετε ότι
να αποδείξετε ότι 
- Αν το διάνυσμα
 είναι μοναδιαίο και ισχύει
είναι μοναδιαίο και ισχύει  να υπολογίσετε την παράσταση
να υπολογίσετε την παράσταση 
- Αν το διάνυσμα
 είναι μοναδιαίο και ισχύει
είναι μοναδιαίο και ισχύει  να αποδείξετε ότι
να αποδείξετε ότι 
- Αν
 και
και  να δείξετε ότι
να δείξετε ότι 
- Αν τα διανύσματα
 είναι μοναδιαία και ισχύει
είναι μοναδιαία και ισχύει  να αποδείξετε ότι
να αποδείξετε ότι 
- Αν
 και
και 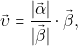 να αποδείξετε ότι:i.).
να αποδείξετε ότι:i.).  και
και 
ii.).
- Αν για τα διανύσματα
 ισχύουν
ισχύουν  και
και  να αποδείξετε ότι
να αποδείξετε ότι 
- Αν
 να δείξετε ότι
να δείξετε ότι 
- Αν
 και
και  και
και  να αποδείξετε ότι:i.).
να αποδείξετε ότι:i.). 
ii.).
ΑΣΚΗΣΕΙΣ ΕΣΩΤΕΡΙΚΟΥ ΓΙΝΟΜΕΝΟΥ ΜΕΡΟΣ Γ.
- Δίνονται τα μη μηδενικά διανύσματα
 για τα οποία ισχύουν
για τα οποία ισχύουν 
i_). Να δείξετε ότι:
ii_). Να βρείτε τη γωνία των
- Αν για τα διανύσματα
 ισχύουν
ισχύουν  και
και  να βρείτε την γωνία
να βρείτε την γωνία 
- Αν
 μοναδιαία και ισχύει
μοναδιαία και ισχύει  να υπολογίσετε την παράσταση
να υπολογίσετε την παράσταση 
- Αν
 και
και  αν υπολογίσετε την τιμή της παράστασης
αν υπολογίσετε την τιμή της παράστασης 
- Αν για τα μη μηδενικά διανύσματα
 ισχύει
ισχύει  και
και  να αποδείξετε ότι:
να αποδείξετε ότι:
i_).
ii_).
- Αν για τα μη μηδενικά διανύσματα
 ισχύει
ισχύει  και
και  να αποδείξετε ότι:
να αποδείξετε ότι:
i_).
ii_)..
- Αν
 και
και 
i_). Να αποδείξετε ότι
ii_). Να βρείτε το διάνυσμα
ΑΣΚΗΣΕΙΣ ΕΣΩΤΕΡΙΚΟΥ ΓΙΝΟΜΕΝΟΥ ΜΕΡΟΣ Γ.
- Αν για κάθε
 τα διανύσματα
τα διανύσματα  και
και  είναι κάθετα μεταξύ τους και
είναι κάθετα μεταξύ τους και  να δείξετε ότι:
να δείξετε ότι:
i_).
ii_).
iii_).
- Έστω τα μοναδιαία διανύσματα
 και το διάνυσμα
και το διάνυσμα  Να βρείτε το
Να βρείτε το  ώστε το
ώστε το  να είναι ελάχιστο. Για την τιμή αυτή του
να είναι ελάχιστο. Για την τιμή αυτή του  να δείξετε ότι το διάνυσμα
να δείξετε ότι το διάνυσμα  είναι κάθετο στο
είναι κάθετο στο 
- Αν
 το διάνυσμα
το διάνυσμα  είναι μοναδιαίο και η εξίσωση
είναι μοναδιαίο και η εξίσωση  έχει διπλή ρίζα, να αποδείξετε ότι
έχει διπλή ρίζα, να αποδείξετε ότι 
- Έστω ότι για τα μη μηδενικά διανύσματα
 ισχύει
ισχύει 
i_). Να αποδείξετε ότι τα είναι συγγραμμικά.
είναι συγγραμμικά. - ii_). Αν τα διανύσματα
 έχουν συντελεστές διεύθυνσης τις ρίζες της εξίσωσης
έχουν συντελεστές διεύθυνσης τις ρίζες της εξίσωσης  να αποδείξετε ότι
να αποδείξετε ότι 
ΑΣΚΗΣΕΙΣ ΕΣΩΤΕΡΙΚΟΥ ΓΙΝΟΜΕΝΟΥ ΜΕΡΟΣ Γ.
- Αν για τα διανύσματα
 ισχύουν
ισχύουν  και
και  να αποδείξετε ότι
να αποδείξετε ότι 
- Δίνονται τα διανύσματα
 και
και  Να βρείτε το διάνυσμα
Να βρείτε το διάνυσμα  ώστε να είναι
ώστε να είναι 
- Αν
 με
με  να αποδείξετε ότι:i_).
να αποδείξετε ότι:i_). 
ii_).
- Έστω τα διανύσματα
 με
με  και ότι για κάθε
και ότι για κάθε  ισχύει
ισχύει  i_). Να δείξετε ότι
i_). Να δείξετε ότι 
ii_). Να βρείτε τα μέτρα των διανυσμάτων και
και 
- Δίνεται τρίγωνο ΑΒΓ. Αν για το σημείο Μ ισχύει
 να δείξετε ότι το Μ κινείται σε μια ευθεία.
να δείξετε ότι το Μ κινείται σε μια ευθεία. - Δίνονται τα σταθερά σημεία Α, Β με
 Να βρείτε το γεωμετρικό τόπο των σημείων Μ, ώστε
Να βρείτε το γεωμετρικό τόπο των σημείων Μ, ώστε 
- Έστω Α, Β δύο σταθερά σημεία με ΑΒ = 3. Να βρείτε το σύνολο των σημείων Μ του επιπέδου, για τα οποία ισχύει

- Έστω τα σημεία Α, Β με (ΑΒ) = 2. Να βρείτε το γεωμετρικό τόπο των σημείων Μ, για τα οποία ισχύει

- Έστω τρίγωνο ΑΒΓ και ΑΔ διάμεσός του. Να βρείτε το γεωμετρικό τόπο των σημείων Μ του επιπέδου, για τα οποία ισχύει:

- Αν
Βιβλιογραφία: Μπάρλας εκδόσεις Ελληνοεκδοτική.

Αυτή η εργασία χορηγείται με άδεια Creative Commons Αναφορά Δημιουργού – Μη Εμπορική Χρήση – Παρόμοια Διανομή 4.0 Διεθνές .
