ΓΡΑΦΙΚΗ ΠΑΡΑΣΤΑΣΗ ΣΥΝΑΡΤΗΣΗΣ
Σημεία γραφικών παραστάσεων συναρτήσεων
- Σημείο ανήκει σε

Ένα σημείο ![]() ανήκει στη γραφική παράσταση μιας συνάρτησης
ανήκει στη γραφική παράσταση μιας συνάρτησης ![]() αν και μόνο αν ισχύει:
αν και μόνο αν ισχύει: ![]()
Σημείο τομής της γραφικης παράστασης της συνάρτησης ![]() με τους άξονες ή με άλλες συναρτήσεις.
με τους άξονες ή με άλλες συναρτήσεις.
Για να βρούμε:
- Το σημείο τομής με τον άξονα

Θέτουμε ![]() και λύνουμε την εξίσωση
και λύνουμε την εξίσωση ![]() . Οι λύσεις της εξίσωσης αυτής θα μας δώσει τα σημεία τομής.
. Οι λύσεις της εξίσωσης αυτής θα μας δώσει τα σημεία τομής.
- Το σημείο τομής με τον άξονα

Θέτουμε ![]() και λύνουμε την εξίσωση
και λύνουμε την εξίσωση ![]() . Το σημείο τομής με τον άξονα
. Το σημείο τομής με τον άξονα ![]() είναι η λύση της εξίσωσης και είναι το
είναι η λύση της εξίσωσης και είναι το ![]() . Εφόσον υπάρχει τέτοιο σημείο αυτό είναι και μοναδικό.
. Εφόσον υπάρχει τέτοιο σημείο αυτό είναι και μοναδικό.
- Τα σημεία τομής δύο συναρτήσεων
 και
και 
Λύνουμε την εξίσωση ![]() και οι ρίζες της εξίσωσης αποτελούν τα κοινά σημεία. Αν η επίλυση των παραπάνω εξισώσεων δεν μας δώσει λύσεις τότε απλά οι συναρτήσεις αυτές δεν έχουν κανένα σημείο τομής.
και οι ρίζες της εξίσωσης αποτελούν τα κοινά σημεία. Αν η επίλυση των παραπάνω εξισώσεων δεν μας δώσει λύσεις τότε απλά οι συναρτήσεις αυτές δεν έχουν κανένα σημείο τομής.
Σχετική θεση γραφικής παράστασης της ![]()
- Με τον άξονα

Για να βρούμε πότε μια συνάρτηση ![]() βρίσκεται πάνω από τον άξονα
βρίσκεται πάνω από τον άξονα ![]() Λύνουμε την ανίσωση
Λύνουμε την ανίσωση ![]() ενώ για κάτω από τον
ενώ για κάτω από τον ![]() λύνουμε την ανίσωση
λύνουμε την ανίσωση ![]()
- Με μια άλλη γραφική παράσταση
Για να βρούμε σε ποιά διαστήματα μια συνάρτηση ![]() είναι πάνω από μια άλλη συνάρτηση
είναι πάνω από μια άλλη συνάρτηση ![]() λύνουμε την ανίσωση
λύνουμε την ανίσωση ![]()
Παράδειγμα.1
Έστω η συνάρτηση ![]() .
.
Να βρεθούν τα κοινά σημεία της ![]()
i) Με τον άξονα ![]()
ii) Με τον άξονα ![]()
iii) Με την συνάρτηση ![]()
Λύση
i) Η ![]() με
με ![]() τέμνει τον
τέμνει τον ![]() για
για ![]() δηλαδή
δηλαδή ![]() άρα έχουμε
άρα έχουμε ![]()
![]()
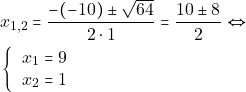
Άρα τα κοινά σημεία με τον ![]() είναι τα
είναι τα ![]() και
και ![]()
ii) Αφου το ![]() τότε η
τότε η ![]() με
με ![]() τέμνει τον
τέμνει τον ![]() για
για ![]() δηλαδή
δηλαδή
![]() οπότε το κοινό σημείο με τον
οπότε το κοινό σημείο με τον ![]() είναι το
είναι το ![]()
iii) Η ![]() με
με ![]() τέμνει την
τέμνει την ![]() με
με ![]() όταν
όταν
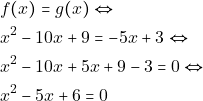
![]()

Οπότε ![]() και
και ![]() και
και
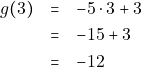
και
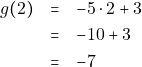
Άρα τα σημεία τομής των ![]() και
και ![]() είναι
είναι ![]() και
και ![]()
Παράδειγμα.2
Έστω η συνάρτηση ![]()
i) Πότε η ![]() βρίσκεται πάνω από τον
βρίσκεται πάνω από τον ![]()
ii) Πότε η ![]() βρίσκεται κάτω από τον
βρίσκεται κάτω από τον ![]()
iii) Πότε η ![]() βρίσκεται πάνω από την
βρίσκεται πάνω από την ![]() με
με ![]()
Λύση
i) Η ![]() με
με ![]() είναι πάνω απο τον
είναι πάνω απο τον ![]() όταν
όταν ![]()

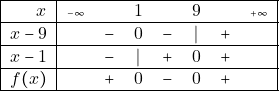
Τελικά η ![]() είναι πάνω απο τον
είναι πάνω απο τον ![]() όταν
όταν ![]() δηλαδή για
δηλαδή για ![]()
ii)Η ![]() με
με ![]() είναι κάτω απο τον
είναι κάτω απο τον ![]() όταν
όταν ![]()
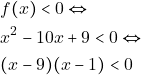
Τελικά η ![]() είναι κάτω απο τον
είναι κάτω απο τον ![]() όταν
όταν ![]() δηλαδή για
δηλαδή για ![]() iii) Η
iii) Η ![]() με
με ![]() είναι πάνω απο την
είναι πάνω απο την ![]() με
με ![]() όταν:
όταν:
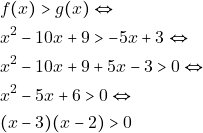

Τελικά η ![]() είναι πάνω απο την
είναι πάνω απο την ![]() όταν
όταν
![]() άρα για
άρα για ![]()
Βιβλιογραφία: Παπαδάκης, εκδόσεις Σαββάλα

Αυτή η εργασία χορηγείται με άδεια Creative Commons Αναφορά Δημιουργού – Μη Εμπορική Χρήση – Παρόμοια Διανομή 4.0 Διεθνές .
