Για να αποδείξουμε ότι δύο συναρτήσεις ![]() είναι ίσες αρκεί να δείξουμε ότι:
είναι ίσες αρκεί να δείξουμε ότι:
Παράδειγμα.1
Να εξετάσετε αν οι συναρτήσεις ![]() είναι ίσες με
είναι ίσες με ![]() και
και ![]()
Λύση
Για την ![]() θα πρέπει
θα πρέπει ![]() επειδή
επειδή ![]() για κάθε
για κάθε ![]() άρα θα πρέπει
άρα θα πρέπει ![]() οπότε
οπότε ![]()
Για την ![]() Θα πρέπει
Θα πρέπει ![]() οπότε
οπότε ![]()
Αφού ![]() δηλαδή οι δυο συναρτήσεις έχουν το ίδιο πεδίο ορισμού για να είναι ίσες οι συναρτήσεις θα πρέπει να έχουν και τον ίδιο αλγεβρικό τύπο δηλαδή,
δηλαδή οι δυο συναρτήσεις έχουν το ίδιο πεδίο ορισμού για να είναι ίσες οι συναρτήσεις θα πρέπει να έχουν και τον ίδιο αλγεβρικό τύπο δηλαδή, ![]()
Έχουμε λοιπόν:
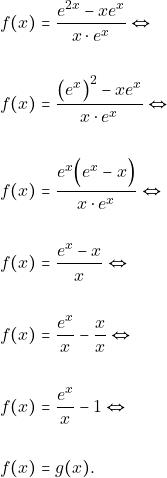
Τελικά αφού οι δύο συναρτήσεις ![]() έχουν το ίδιο πεδίο ορισμού και το ίδιο αλγεβρικό τύπο, άρα οι δύο αυτές συναρτήσεις είναι ίσες δηλαδη
έχουν το ίδιο πεδίο ορισμού και το ίδιο αλγεβρικό τύπο, άρα οι δύο αυτές συναρτήσεις είναι ίσες δηλαδη ![]()
Παράδειγμα.2
Να εξετάσετε αν οι συναρτήσεις ![]() και
και ![]() είναι ίσες. Αν δεν είναι ίσες να βρείτε το ευρύτερο υποσύνολο του
είναι ίσες. Αν δεν είναι ίσες να βρείτε το ευρύτερο υποσύνολο του ![]() στο οποίο είναι ίσες.
στο οποίο είναι ίσες.
Λύση
Η συνάρτηση
![]()
ορίζεται όταν:
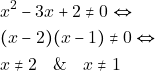
Άρα το πεδίο ορισμού της ![]() είναι το σύνολο
είναι το σύνολο
![]()
Η συνάρτηση
![]()
ορίζεται όταν:
![]()
Άρα το πεδίο ορισμού της ![]() είναι το σύνολο
είναι το σύνολο
![]()
Παρατηρούμε ![]() , άρα οι συναρτήσεις
, άρα οι συναρτήσεις ![]() και
και ![]() δεν είναι ίσες.
δεν είναι ίσες.
Αν όμως ![]() , τότε ισχύει:
, τότε ισχύει:
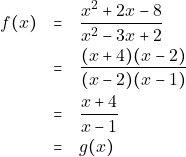
Άρα για ![]() ισχύει ότι οι συναρτήσεις
ισχύει ότι οι συναρτήσεις ![]() και
και ![]() είναι ίσες.
είναι ίσες.
Βιβλιογραφία Μπάρλας εκδόσεις Ελληνοεκδοτική, Παπαδάκης εκδόσεις Σαββάλα.

Αυτή η εργασία χορηγείται με άδεια Creative Commons Αναφορά Δημιουργού – Μη Εμπορική Χρήση – Παρόμοια Διανομή 4.0 Διεθνές .
