Έστω δύο συναρτήσεις ![]() με πεδία ορισμού
με πεδία ορισμού ![]() και
και ![]() αντίστοιχα. Τότε οι πράξεις του αθροίσματος, διαφοράς, γινόμενου και πηλίκου ορίζονται ως εξής:
αντίστοιχα. Τότε οι πράξεις του αθροίσματος, διαφοράς, γινόμενου και πηλίκου ορίζονται ως εξής:
Παράδειγμα.1
Δίνονται οι συναρτήσεις ![]() και
και ![]() Να ορίσετε τις συναρτήσεις
Να ορίσετε τις συναρτήσεις ![]() και
και ![]()
Λύση
Αρχικά θα βρούμε τα πεδία ορισμού των συναρτήσεων ![]() και
και ![]()
Η συνάρτηση ![]() ορίζεται όταν
ορίζεται όταν
![]()
Άρα το πεδίο ορισμού της συνάρτησης ![]() είναι το σύνολο
είναι το σύνολο
![]()
Η συνάρτηση
![]()
ορίζεται όταν
![]()
Άρα το πεδίο ορισμού της συνάρτησης ![]() είναι το σύνολο
είναι το σύνολο
![]()
Οι συναρτήσεις ![]() έχουν πεδίο ορισμού τα κοινά σημεία των
έχουν πεδίο ορισμού τα κοινά σημεία των ![]() και
και ![]() δηλαδή το σύνολο
δηλαδή το σύνολο
![]()
και τύπους αντίστοιχα
![]()
![]()
![]()
Τέλος έχουμε
![]()
Άρα η συνάρτηση ![]() έχει πεδίο ορισμού τα κοινά σημεία των
έχει πεδίο ορισμού τα κοινά σημεία των ![]() και
και ![]() εκτός απο τα σημεια που μηδενίζουν τον παρονομαστή, δηλαδή:
εκτός απο τα σημεια που μηδενίζουν τον παρονομαστή, δηλαδή:
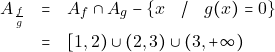
και τύπο
![Rendered by QuickLaTeX.com \[\bigg(\dfrac{f}{g}\bigg)(x) =\dfrac{f(x)}{g(x)} =\dfrac{\sqrt{x-1}}{\frac{x^2-4}{x^2-3x}} =\dfrac{(x^2-3x)\sqrt{x-1}}{x^2-4}\]](https://study4maths.gr/wp-content/ql-cache/quicklatex.com-9ff4502fe157e889ecc1a61feae62eb3_l3.png)
Παράδειγμα.2
Δίνονται οι συναρτήσεις
![]()
και
![]()
Να ορίσετε τη συνάρτηση ![]()
Λύση
Οι πράξεις μεταξύ συναρτήσεων ορίζονται στα κοινά σημεία του πεδίου ορισμού τους. Άρα έχουμε:
Για ![]()
![]()
Για ![]()
![]()
Για ![]()
![]()
Άρα έχουμε ότι:
![Rendered by QuickLaTeX.com \[(f+g)(x)= \left\{ \begin{tabular}{ll} $-2, \quad x \leq -1$ \\ $2x-3, \quad -1<x \leq 2$ \\ $4x-1, \quad x>2$\\ \end{tabular} \right. \]](https://study4maths.gr/wp-content/ql-cache/quicklatex.com-0d3139b2e730975d2eb71006aad76804_l3.png)
Βιβλιογραφία: Παπαδάκης, εκδόσεις Σαββάλα

Αυτή η εργασία χορηγείται με άδεια Creative Commons Αναφορά Δημιουργού – Μη Εμπορική Χρήση – Παρόμοια Διανομή 4.0 Διεθνές .

Ευχαριστώ