Σχέσεις που δεν ισχύουν πάντα

ΛΥΣΗ
α) Επειδή το εσωτερικό γινόμενο δύο διανυσμάτων ![]() είναι αριθμός τότε το
είναι αριθμός τότε το ![]() είναι η απόλυτη τιμή πραγματικού αριθμού ενώ το
είναι η απόλυτη τιμή πραγματικού αριθμού ενώ το ![]() είναι το γινόμενο των μέτρων των διανυσμάτων
είναι το γινόμενο των μέτρων των διανυσμάτων ![]() και
και ![]()
Αν για παράδειγμα, είναι
![]()
τότε:
![]()
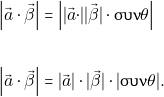
Επειδή ισχύει ![]() διακρίνουμε τις περιπτωσεις:
διακρίνουμε τις περιπτωσεις:
ΠΕΡ.1.
Aν ![]() τότε
τότε ![]() και
και ![]()
Aν ![]() τότε
τότε ![]() και
και ![]()
δηλαδη έχουμε ![]() και
και ![]() και θα ισχύει:
και θα ισχύει:
![]()
![]()
![]()
ΠΕΡ.2.
Αν ![]() και
και ![]() τοτε
τοτε ![]()
οπότε ![]() με
με ![]() δηλαδή
δηλαδή ![]()
άρα θα ισχύει:
![]()
![]()
ΠΕΡ.3.
Αν ![]() τοτε
τοτε ![]() και
και ![]()
άρα θα έχουμε:
![]()
![]()
Από ΠΕΡ.1. ΠΕΡ.2. και ΠΕΡ.3 έχουμε ότι:
![]()
ΤΟ ΙΣΟΝ ![]() ΙΣΧΥΕΙ ΟΤΑΝ
ΙΣΧΥΕΙ ΟΤΑΝ ![]() ΜΟΝΟΝ
ΜΟΝΟΝ
β) Ομοίως έχουμε:
![]()
![]()
![]()
![]()
Παίρνοντας τις ίδιες περιπτώσεις για την γωνία ![]() οπώς στο ερώτημα α)
οπώς στο ερώτημα α)
έχουμε: αν ![]() δηλαδή αν
δηλαδή αν ![]()
![]()
![]()
Γενικά για οποιαδήποτε διανύσματα ![]() και
και ![]() ισχύει:
ισχύει:
![]()
Η ισότητα ![]() ισχύει όταν
ισχύει όταν ![]() δηλαδή όταν
δηλαδή όταν ![]()
γ) Αν θέσουμε
![]()
τότε η ισότητα:
![]()
γίνεται:
![]()
η οποία ισχύει μόνο αν ![]() ή
ή ![]()
Βιβλιογραφία:
Παπαδάκης εκδόσεις Σαββάλα.

Αυτή η εργασία χορηγείται με άδεια Creative Commons Αναφορά Δημιουργού – Μη Εμπορική Χρήση – Παρόμοια Διανομή 4.0 Διεθνές .
