Ιδιότητες εσωτερικού γινομένου
Για τα διανύσματα  και
και  ισχύουν οι εξής ιδιότητες:
ισχύουν οι εξής ιδιότητες:
-

-

-
 εφόσον
εφόσον 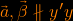
Ιδιότητες εσωτερικού γινομένου
Σχέσεις που δεν ισχύουν πάντα

ΛΥΣΗ
Συνέχεια ανάγνωσης ΙΣΟΤΗΤΕΣ ΕΣΩΤΕΡΙΚΟΥ ΓΙΝΟΜΕΝΟΥ ΚΑΙ ΜΕΤΡΟΥ ΔΙΑΝΥΣΜΑΤΩΝ ΠΟΥ ΔΕΝ ΙΣΧΥΟΥΝ ΠΑΝΤΑ
ΕΣΩΤΕΡΙΚΟ ΓΙΝΟΜΕΝΟ ΚΑΙ ΑΠΟΔΕΙΚΤΙΚΕΣ ΑΣΚΗΣΕΙΣ

Συνέχεια ανάγνωσης ΕΣΩΤΕΡΙΚΟ ΓΙΝΟΜΕΝΟ ΚΑΙ ΑΠΟΔΕΙΚΤΙΚΕΣ ΑΣΚΗΣΕΙΣ
Ισότητα μέτρων
![]()
Υπολογισμός μέτρου της μορφής ![]()
Συνέχεια ανάγνωσης ΜΕΤΡΟ ΓΡΑΜΜΙΚΟΥ ΣΥΝΔΥΑΣΜΟΥ ΔΥΟ ΔΙΑΝΥΣΜΑΤΩΝ
Κριτήριο για ομόρροπα ή αντίρροπα διανύσματα