ΙΔΙΟΤΗΤΕΣ ΕΣΩΤΕΡΙΚΟΥ ΓΙΝΟΜΕΝΟΥ

Ιδιότητες εσωτερικού γινομένου

Για τα διανύσματα $\vec{α},\vec{\beta}$ και $\vec{\gamma}$ ισχύουν οι εξής ιδιότητες:

$\color{violet}{(\lambda \vec{α}) \cdot \vec{\beta} = \vec{α} \cdot (\lambda \vec{\beta}) = \lambda (\vec{α} \cdot \vec{\beta}), \lambda \in \mathbb{R}}$
$\color{magenta}{\vec{α} \cdot (\vec{\beta + \gamma}) = \vec{α} \cdot \vec{\beta} + \vec{α} \cdot \vec{\gamma}}$
$\color{orange}{\vec{α} \perp \vec{\beta} \Leftrightarrow \lambda_{\vec{α}} \lambda_{\vec{\beta}} = -1,$ εφόσον $\color{orange}{\vec{α}, \vec{\beta} \nparallel y'y}}$

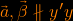
ΑΠΟΔΕΙΞΗ
Έστω ότι είναι:

$\vec{α} = (\mathrm{x}_{1},\mathrm{y}_{1}),$

$\vec{\beta} = (\mathrm{x}_{2},\mathrm{y}_{1})$

και

$\vec{\gamma} = (\mathrm{x}_{3},\mathrm{y}_{3}).$

1.) Έχουμε:

$\begin{align*} (\lambda \vec{α}) \cdot \vec{\beta} &= (\lambda \mathrm{x}_{1}, \lambda \mathrm{y}_{1}) \cdot (\mathrm{x}_{2}, \mathrm{y}_{2}) \\ &= \lambda \mathrm{x}_{1}\mathrm{x}_{2} + \lambda \mathrm{y}_{1}\mathrm{y}_{2} \\ &= \lambda (\mathrm{x}_{1} \mathrm{x}_{2}+\mathrm{y}_{1} \mathrm{y}_{2}) \\ &= \lambda (\vec{α} \cdot \vec{\beta}) \quad (1) \end{align*}$

επισης

$\begin{align*} \vec{α} \cdot (\lambda \vec{\beta}) &= (\mathrm{x}_{1}, \mathrm{y}_{1}) \cdot (\lambda \mathrm{x}_{2}, \lambda \mathrm{y}_{2})\\ &= \lambda \mathrm{x}_{1} \mathrm{x}_{2} + \lambda \mathrm{y}_{1}\mathrm{y}_{2} \\ &= \lambda (\mathrm{x}_{1} \mathrm{x}_{2}+\mathrm{y}_{1} \mathrm{y}_{2}) \\\ &= \lambda (\vec{α} \cdot \vec{\beta}) \quad (1) \end{align*}$

από $(1)$ και $(2)$ έχουμε:

$(\lambda \vec{α}) \cdot \vec{\beta} = \vec{α} \cdot (\lambda \vec{\beta}) = \lambda (\vec{α} \cdot \vec{\beta}), \lambda \in \mathbb{R}}$

2.) Έχουμε:

$\vec{α} \cdot (\vec{\beta + \gamma}) =$

$(\mathrm{x}_{1}, \mathrm{y}_{1}) \cdot\Big[ (\mathrm{x}_{2}\, , \, \mathrm{y}_{2}) +(\mathrm{x}_{3}\, , \, \mathrm{y}_{3}) \Big ]=$

$(\mathrm{x}_{1}, \mathrm{y}_{1}) \cdot (\mathrm{x}_{2} + \mathrm{x}_{3}\, , \, \mathrm{y}_{2} + \mathrm{y}_{3}) =$

$\mathrm{x}_{1} (\mathrm{x}_{2}+\mathrm{x}_{3}) + \mathrm{y}_{1} (\mathrm{y}_{2} + \mathrm{y}_{3})=$

$\mathrm{x}_{1} \mathrm{x}_{2} + \mathrm{x}_{1} \mathrm{x}_{3} + \mathrm{y}_{1} \mathrm{y}_{2} + \mathrm{y}_{1} \mathrm{y}_{3} =$

$(\mathrm{x}_{1} \mathrm{x}_{2} + \mathrm{y}_{1} \mathrm{y}_{2}) + (\mathrm{x}_{1} \mathrm{x}_{3} + \mathrm{y}_{1} \mathrm{y}_{3}) =$

$\vec{α} \cdot \vec{\beta} + \vec{α} \cdot \vec{\gamma}$

3.)

Αφού $\vec{α}, \vec{\beta} \nparallel y'y,$ και $\vec{α} = (\mathrm{x}_{1},\mathrm{y}_{1}),$
$\vec{\beta} = (\mathrm{x}_{2},\mathrm{y}_{1}),$ θα ισχύει ότι $\mathrm{x}_{1}, \mathrm{x}_{2} \neq 0.$ Έχουμε:

$\vec{α} \perp \vec{\beta}$

$\vec{α} \cdot \vec{\beta} = 0$

$\mathrm{x}_{1}, \mathrm{y}_{1}) \cdot (\mathrm{x}_{2}, \mathrm{y}_{2} = 0$

$(\mathrm{x}_{1}, \mathrm{y}_{1}) \cdot (\mathrm{x}_{2}, \mathrm{y}_{2}) = 0$

$\mathrm{x}_{1}\mathrm{x}_{2}+\mathrm{y}_{1}\mathrm{y}_{2} = 0$

$\mathrm{y}_{1}\mathrm{y}_{2} = -\mathrm{x}_{1}\mathrm{x}_{2}$

$\frac{\mathrm{y}_{1}}{\mathrm{x}_{1}} \cdot \frac{\mathrm{y}_{2}}{\mathrm{x}_{2}} = -1$

$\lambda_{\vec{α}} \lambda_{\vec{\beta}} = -1$

Rendered by QuickLaTeX.com

ΛΥΣΗ

Υπολογίζουμε αρχικά το εσωτερικό γινόμενο $\vec{α} \cdot \vec{\beta}.$
Είναι:

$\vec{α} \cdot \vec{\beta} = \lvert \vec{α} \rvert \lvert \vec{\beta} \rvert \cdot \sigma \upsilon \nu(\widehat{\vec{α}, \vec{\beta}}) \Leftrightarrow$

$\vec{α} \cdot \vec{\beta} = 2 \cdot 3\cdot \sigma \upsilon \nu60^{\circ} \Leftrightarrow$

$\vec{α} \cdot \vec{\beta} = 6 \cdot \frac{1}{2} \Leftrightarrow$

$\vec{α} \cdot \vec{\beta} = 3.$

Σημείωση
Από την επιμεριστική ιδιότητα:

$\vec{α} \cdot (\vec{\beta} + \vec{\gamma}) = \vec{α} \cdot \vec{\beta} + \vec{α} \cdot \vec{\gamma}$

προκύπτει ότι μπορούμε να αναπτύσσουμε παραστάσεις της μορφής:

$(\kappa \vec{α} + \lambda \vec{\beta}) \cdot (\mu \vec{α} + \nu \vec{\beta}) \quad \text{ή} \quad (\kappa \vec{α} + \lambda \vec{\beta})^{2}$

όπως στους πραγματικούς αριθμούς.
Δηλαδή:

$(\kappa \vec{α} + \lambda \vec{\beta}) \cdot (\mu \vec{α} + \nu \vec{\beta}) = \kappa \mu \vec{α}^{2} + \lambda \mu \vec{\beta} \cdot \vec{α} + \kappa \nu \vec{α} \cdot \vec{\beta} + \lambda \nu \vec{\beta}^{2}$