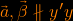Αρχείο ετικέτας ΔΙΑΝΥΣΜΑΤΑ

Β ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ / ΠΡΟΣΘΕΣΗ ΚΑΙ ΑΦΑΙΡΕΣΗ ΔΙΑΝΥΣΜΑΤΩΝ

ΚΑΝΟΝΕΣ ΠΡΟΣΘΕΣΗΣ ΔΙΑΝΥΣΜΑΤΩΝ

1 σχόλιο

ΚΑΝΟΝΕΣ ΠΡΟΣΘΕΣΗΣ ΔΙΑΝΥΣΜΑΤΩΝ

Συνέχεια ανάγνωσης ΚΑΝΟΝΕΣ ΠΡΟΣΘΕΣΗΣ ΔΙΑΝΥΣΜΑΤΩΝ →

Β ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ / ΑΣΚΗΣΕΙΣ ΣΧΟΛΙΚΟΥ ΓΙΝΟΜΕΝΟ ΑΡΙΘΜΟΥ ΜΕ ΔΙΑΝΥΣΜΑ

ΣΧΟΛΙΚΟ ΑΣΚΗΣΗ 2 Β ΟΜΑΔΑ

Σχολιάστε

ΣΧΟΛΙΚΟ ΑΣΚΗΣΗ 2 Β ΟΜΑΔΑ

Για να επιλύσετε τις παρακάτω ασκήσεις θα πρέπει να έχετε διαβάσει την αντίστοιχη θεωρία που βρίσκεται στον παρακάτω σύνδεσμο:
ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ ΑΡΙΘΜΟΥ ΜΕ ΔΙΑΝΥΣΜΑ

Άσκηση 2 Β ομάδας σελίδα 28 σχολικού βιβλίου Μαθηματικά προσανατολισμού Β λυκείου

Συνέχεια ανάγνωσης ΣΧΟΛΙΚΟ ΑΣΚΗΣΗ 2 Β ΟΜΑΔΑ →

Β ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ / ΑΣΚΗΣΕΙΣ ΣΧΟΛΙΚΟΥ ΓΙΝΟΜΕΝΟ ΑΡΙΘΜΟΥ ΜΕ ΔΙΑΝΥΣΜΑ

Α ΟΜΑΔΑ ΑΣΚΗΣΕΙΣ 1 ΕΩΣ 5

Σχολιάστε

Α ΟΜΑΔΑ ΑΣΚΗΣΕΙΣ 1 ΕΩΣ 5
Για να επιλύσετε τις παρακάτω ασκήσεις θα πρέπει να έχετε διαβάσει την αντίστοιχη θεωρία που βρίσκεται στον παρακάτω σύνδεσμο:
ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ ΑΡΙΘΜΟΥ ΜΕ ΔΙΑΝΥΣΜΑ

Άσκηση 1 σελίδα 26 σχολικού βιβλίου Μαθηματικά προσανατολισμού Β λυκείου

Συνέχεια ανάγνωσης Α ΟΜΑΔΑ ΑΣΚΗΣΕΙΣ 1 ΕΩΣ 5 →

Β ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ / ΑΣΚΗΣΕΙΣ ΣΧΟΛΙΚΟΥ ΠΡΟΣΘΕΣΗ ΚΑΙ ΑΦΑΙΡΕΣΗ ΔΙΑΝΥΣΜΑΤΩΝ

ΑΣΚ3 ΑΘΡΟΙΣΜΑ ΔΙΑΔΟΧΙΚΩΝ ΔΙΑΝΥΣΜΑΤΩΝ

Σχολιάστε

ΑΣΚ3 ΑΘΡΟΙΣΜΑ ΔΙΑΔΟΧΙΚΩΝ ΔΙΑΝΥΣΜΑΤΩΝ

ΑΣΚ3  ΑΘΡΟΙΣΜΑ ΔΙΑΔΟΧΙΚΩΝ ΔΙΑΝΥΣΜΑΤΩΝ

Να εκφράσετε το διάνυσμα \vec{x} σε καθένα από τα παρακάτω σχήματα ως συνάρτηση των άλλων διανυσμάτων που δίνονται:

Διανύσματα σε κλειστή “διαδρομή”

ΛΥΣΗ

Συνέχεια ανάγνωσης ΑΣΚ3 ΑΘΡΟΙΣΜΑ ΔΙΑΔΟΧΙΚΩΝ ΔΙΑΝΥΣΜΑΤΩΝ →

Β ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ / ΑΣΚΗΣΕΙΣ ΣΧΟΛΙΚΟΥ ΠΡΟΣΘΕΣΗ ΚΑΙ ΑΦΑΙΡΕΣΗ ΔΙΑΝΥΣΜΑΤΩΝ

ΑΣΚ4 ΙΣΑ ΔΙΑΝΥΣΜΑΤΑ ΣΕ ΠΑΡΑΛΛΗΛΟΓΡΑΜΜΟ

Σχολιάστε

ΑΣΚ4 ΙΣΑ ΔΙΑΝΥΣΜΑΤΑ ΣΕ ΠΑΡΑΛΛΗΛΟΓΡΑΜΜΟ

ΔΙΑΝΥΣΜΑΤΙΚΗ ΙΣΟΤΗΤΑ
ΑΣΚΗΣΗ 4 ΣΕΛΙΔΑ 21 ΣΧΟΛΙΚΟ ΒΙΒΛΙΟ ΜΑΘΗΜΑΤΙΚΑ Β ΛΥΚΕΙΟΥ

ΛΥΣΗ

Συνέχεια ανάγνωσης ΑΣΚ4 ΙΣΑ ΔΙΑΝΥΣΜΑΤΑ ΣΕ ΠΑΡΑΛΛΗΛΟΓΡΑΜΜΟ →

Β ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ / ΕΣΩΤΕΡΙΚΟ ΓΙΝΟΜΕΝΟ ΔΙΑΝΥΣΜΑΤΩΝ

ΕΣΩΤΕΡΙΚΟ ΓΙΝΟΜΕΝΟ

Σχολιάστε

ΕΣΩΤΕΡΙΚΟ ΓΙΝΟΜΕΝΟ


Εσωτερικό γινόμενο διανυσμάτων
Ορισμός
Ονομάζουμε εσωτερικό γινόμενο δύο μη μηδενικών διανυσμάτων \vec{\boldsymbol{α}} και \vec{\boldsymbol{\beta}}, και το συμβολίζουμε με \vec{\boldsymbol{α}} \cdot \vec{\boldsymbol{\beta}}, τον πραγματικό αριθμό:

    \[\vec{α} \cdot \vec{\beta}=\lvert{\vec{α}}\rvert \lvert{\vec{\beta}}\rvert \sigma \upsilon \nu \phi\]


Συνέχεια ανάγνωσης ΕΣΩΤΕΡΙΚΟ ΓΙΝΟΜΕΝΟ →

Β ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ / ΑΣΚΗΣΕΙΣ ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ ΑΡΙΘΜΟΥ ΜΕ ΔΙΑΝΥΣΜΑ

ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ ΑΡΙΘΜΟΥ ΕΠΙ ΔΙΑΝΥΣΜΑ

Σχολιάστε
  1. Δίνονται τα διανύσματα \vec{\alpha}, \vec{\beta} στο επόμενο σχήμα.

    Να κατασκευάσετε τα διανύσματα: 2\vec{\alpha}, ~-\dfrac{1}{2}\vec{\beta}, ~-\vec{\alpha} + 2\vec{\beta}

    2. Συνέχεια ανάγνωσης ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ ΑΡΙΘΜΟΥ ΕΠΙ ΔΙΑΝΥΣΜΑ →

Β ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ / ΑΣΚΗΣΕΙΣ ΠΡΟΣΘΕΣΗ ΚΑΙ ΑΦΑΙΡΕΣΗ ΔΙΑΝΥΣΜΑΤΩΝ

ΠΡΟΣΘΕΣΗ ΚΑΙ ΑΦΑΙΡΕΣΗ ΔΙΑΝΥΣΜΑΤΩΝ

Σχολιάστε

ΠΡΟΣΘΕΣΗ ΚΑΙ ΑΦΑΙΡΕΣΗ ΔΙΑΝΥΣΜΑΤΩΝ

  1.  Δίνεται τρίγωνο ΑΒΓ. Να βρείτε τα αθροίσματα:
    i) \overrightarrow{AB} + \overrightarrow{A\Gamma}
    ii)\overrightarrow{A\Gamma} + \overrightarrow{B\Gamma}
  2.  Να εκφράσετε το διάνυσμα \vec{x} ως συνάρτηση των άλλων διανυσμάτων που δίνονται.

    3. Συνέχεια ανάγνωσης ΠΡΟΣΘΕΣΗ ΚΑΙ ΑΦΑΙΡΕΣΗ ΔΙΑΝΥΣΜΑΤΩΝ →

Β ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ / ΕΣΩΤΕΡΙΚΟ ΓΙΝΟΜΕΝΟ ΔΙΑΝΥΣΜΑΤΩΝ

ΑΝΑΛΥΤΙΚΗ ΕΚΦΡΑΣΗ ΕΣΩΤΕΡΙΚΟΥ ΓΙΝΟΜΕΝΟΥ

Σχολιάστε

ΑΝΑΛΥΤΙΚΗ ΕΚΦΡΑΣΗ ΕΣΩΤΕΡΙΚΟΥ ΓΙΝΟΜΕΝΟΥ

Αν \vec{α}=(\mathrm{x_1},\mathrm{y_1}) και \vec{\beta}=(\mathrm{x_2},\mathrm{y_2}) δύο διανύσματα του Καρτεσιανού επιπέδου, τότε:

    \[\vec{α} \cdot \vec{\beta}=\mathrm{x_1}\mathrm{x_2}+\mathrm{y_1}\mathrm{y_2}\]

Δηλαδή:
Το εσωτερικό γινόμενο δύο διανυσμάτων είναι ίσο με το άθροισμα των γινομένων των ομωνύμων συντεταγμένων τους.

Συνέχεια ανάγνωσης ΑΝΑΛΥΤΙΚΗ ΕΚΦΡΑΣΗ ΕΣΩΤΕΡΙΚΟΥ ΓΙΝΟΜΕΝΟΥ →

Β ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ / ΕΣΩΤΕΡΙΚΟ ΓΙΝΟΜΕΝΟ ΔΙΑΝΥΣΜΑΤΩΝ

ΙΔΙΟΤΗΤΕΣ ΕΣΩΤΕΡΙΚΟΥ ΓΙΝΟΜΕΝΟΥ

Σχολιάστε

ΙΔΙΟΤΗΤΕΣ ΕΣΩΤΕΡΙΚΟΥ ΓΙΝΟΜΕΝΟΥ

Για τα διανύσματα \vec{α},\vec{\beta} και \vec{\gamma} ισχύουν οι εξής ιδιότητες:

  1.  \color{violet}{(\lambda \vec{α}) \cdot \vec{\beta} = \vec{α} \cdot (\lambda \vec{\beta}) = \lambda (\vec{α} \cdot \vec{\beta}), \lambda \in \mathbb{R}}
  2.  \color{magenta}{\vec{α} \cdot (\vec{\beta + \gamma}) = \vec{α} \cdot \vec{\beta} + \vec{α} \cdot \vec{\gamma}}
  3.  \color{orange}{\vec{α} \perp \vec{\beta} \Leftrightarrow \lambda_{\vec{α}} \lambda_{\vec{\beta}} = -1, εφόσον \color{orange}{\vec{α}, \vec{\beta} \nparallel y'y}}

Συνέχεια ανάγνωσης ΙΔΙΟΤΗΤΕΣ ΕΣΩΤΕΡΙΚΟΥ ΓΙΝΟΜΕΝΟΥ →