Άρθρα ανά μήνα: Νοέμβριος 2020

Γ Λυκείου / Η ΕΝΝΟΙΑ ΤΗΣ ΠΑΡΑΓΩΓΟΥ ΑΣΚΗΣΕΙΣ

ΟΡΙΣΜΟΣ ΠΑΡΑΓΩΓΟΥ ΚΑΙ ΤΕΧΝΑΣΜΑ ΣΤΟ ΟΡΙΟ

Σχολιάστε

ΟΡΙΣΜΟΣ ΠΑΡΑΓΩΓΟΥ ΚΑΙ ΤΕΧΝΑΣΜΑ ΣΤΟ ΟΡΙΟ

Rendered by QuickLaTeX.com

Λύση

Συνέχεια ανάγνωσης ΟΡΙΣΜΟΣ ΠΑΡΑΓΩΓΟΥ ΚΑΙ ΤΕΧΝΑΣΜΑ ΣΤΟ ΟΡΙΟ →

Β ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ / ΓΕΝΙΚΗ ΜΟΡΦΗ ΕΞΙΣΩΣΗ ΕΥΘΕΙΑΣ

ΔΕΥΤΕΡΟΥ ΒΑΘΜΟΥ ΕΞΙΣΩΣΗ ΩΣ ΠΡΟΣ X KAI Y

Σχολιάστε

ΔΕΥΤΕΡΟΥ ΒΑΘΜΟΥ ΕΞΙΣΩΣΗ ΩΣ ΠΡΟΣ X KAI Y

Εξισώσεις της μορφής

    \[\boldsymbol{A\mathrm{x}^{2} + B\mathrm{y}^{2} + \Gamma \mathrm{x}\mathrm{y} + \Delta\mathrm{x} + E\mathrm{y} + Z = 0}\]


Για να αποδείξουμε ότι μια εξίσωση της μορφής:

    \[A\mathrm{x}^{2} + B\mathrm{y}^{2} + \Gamma \mathrm{x}\mathrm{y} + \Delta\mathrm{x} + E\mathrm{y} + Z = 0\]

παριστάνει δύο ευθείες, εργαζόμαστε ως εξής:
Θεωρούμε ότι η εξίσωση είναι τριώνυμο ως προς \mathrm{x} (ή ως προς \mathrm{y},) δηλαδή:

    \[A\mathrm{x}^{2} + (\Gamma \mathrm{y} + \Delta)\mathrm{x}+ B\mathrm{y}^{2} + E\mathrm{y} + Z = 0\]

Λύνουμε την παραπάνω εξίσωση και βρίσκουμε δύο σχέσεις ανάμεσα στα \mathrm{x} και \mathrm{y}, οι οποίες είναι οι εξισώσεις των ζητούμενων ευθειών

Συνέχεια ανάγνωσης ΔΕΥΤΕΡΟΥ ΒΑΘΜΟΥ ΕΞΙΣΩΣΗ ΩΣ ΠΡΟΣ X KAI Y →

Γ Λυκείου / ΣΥΝΕΠΕΙΕΣ BOLZANO ΑΣΚΗΣΕΙΣ

ΑΣΚΗΣΗ ΘΕΩΡΗΜΑ ΜΕΓΙΣΤΗΣ ΚΑΙ ΕΛΑΧΙΣΤΗΣ ΤΙΜΗΣ 51.59

Σχολιάστε

ΑΣΚΗΣΗ ΘΕΩΡΗΜΑ ΜΕΓΙΣΤΗΣ ΚΑΙ ΕΛΑΧΙΣΤΗΣ ΤΙΜΗΣ 51.59

Rendered by QuickLaTeX.com

Συνέχεια ανάγνωσης ΑΣΚΗΣΗ ΘΕΩΡΗΜΑ ΜΕΓΙΣΤΗΣ ΚΑΙ ΕΛΑΧΙΣΤΗΣ ΤΙΜΗΣ 51.59 →

Γ Λυκείου / ΣΥΝΕΠΕΙΕΣ BOLZANO ΑΣΚΗΣΕΙΣ

ΑΣΚΗΣΗ ΘΕΩΡΗΜΑ ΕΝΔΙΑΜΕΣΩΝ ΤΙΜΩΝ 65.61

Σχολιάστε

ΑΣΚΗΣΗ ΘΕΩΡΗΜΑ ΕΝΔΙΑΜΕΣΩΝ ΤΙΜΩΝ 65.61

Rendered by QuickLaTeX.com

Συνέχεια ανάγνωσης ΑΣΚΗΣΗ ΘΕΩΡΗΜΑ ΕΝΔΙΑΜΕΣΩΝ ΤΙΜΩΝ 65.61 →

Β ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ / Η ΕΞΙΣΩΣΗ ΤΗΣ ΕΥΘΕΙΑΣ ΣΤΟ ΕΠΙΠΕΔΟ

ΚΛΙΣΗ – ΣΥΝΤΕΛΕΣΤΗΣ ΔΙΕΥΘΥΝΣΗΣ ΕΥΘΕΙΑΣ

Σχολιάστε

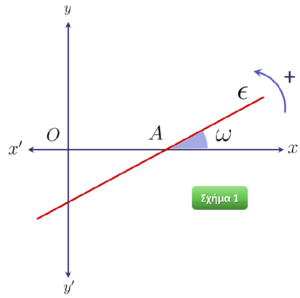
ΚΛΙΣΗ –  ΣΥΝΤΕΛΕΣΤΗΣ ΔΙΕΥΘΥΝΣΗΣ ΕΥΘΕΙΑΣ

Γωνία που σχηματίζει ευθεία με τον άξονα  \boldsymbol{x'x}

Σε ένα σύστημα συντεταγμένων Oxy θεωρούμε μια ευθεία (\epsilon) που τέμνει τον άξονα x'x στο σημείο Α.

Η γωνία \omega που διαγράφει ο άξονας x'x όταν στραφεί γύρω από το Α κατά τη θετική φορά, μέχρι να συμπέσει με την ευθεία (\epsilon), ονομάζεται γωνία που σχηματίζει η ευθεία \boldsymbol{(\epsilon)} με τον άξονα \boldsymbol{x'x} (σχήμα 1).

Γωνία που σχηματίζει ευθεία με τον άξονα \boldsymbol{x'x}

Συνέχεια ανάγνωσης ΚΛΙΣΗ – ΣΥΝΤΕΛΕΣΤΗΣ ΔΙΕΥΘΥΝΣΗΣ ΕΥΘΕΙΑΣ →

Β ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ / ΑΣΚΗΣΕΙΣ ΕΣΩΤΕΡΙΚΟ ΓΙΝΟΜΕΝΟ

ΑΣΚΗΣΕΙΣ ΕΣΩΤΕΡΙΚΟΥ ΓΙΝΟΜΕΝΟΥ ΜΕΡΟΣ Α.

Σχολιάστε

ΑΣΚΗΣΕΙΣ ΕΣΩΤΕΡΙΚΟΥ ΓΙΝΟΜΕΝΟΥ ΜΕΡΟΣ Α.

    1. Αν το διάνυσμα \vec{\alpha} είναι μοναδιαίο, |\vec{\beta}| = 2 και (\widehat{\vec{\alpha}, \vec{\beta}}) = \dfrac{2\pi}{3}, να υπολογίσετε τα εσωτερικά γινόμενα:i_). \vec{\alpha} \cdot \vec{\beta},
      ii_). (\vec{\alpha} - 2\vec{\beta}) \cdot (\vec{\alpha} - \vec{\beta}),
      iii_). (\vec{\alpha} - 3\vec{\beta})^2.

      2. Συνέχεια ανάγνωσης ΑΣΚΗΣΕΙΣ ΕΣΩΤΕΡΙΚΟΥ ΓΙΝΟΜΕΝΟΥ ΜΕΡΟΣ Α. →

Β ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ / ΑΣΚΗΣΕΙΣ ΕΣΩΤΕΡΙΚΟ ΓΙΝΟΜΕΝΟ

ΑΣΚΗΣΕΙΣ ΕΣΩΤΕΡΙΚΟΥ ΓΙΝΟΜΕΝΟΥ ΜΕΡΟΣ Β.

Σχολιάστε
  1. Αν \vec{\alpha} = (3, \sqrt{3}) και \vec{\beta} = (\sqrt{3}, -1) να βρείτε τη γωνία των \vec{\alpha}, \vec{\beta}.
  2. Αν \vec{\alpha} = (1, \sqrt{3}) και \vec{\beta} = (-\sqrt{3}, 3) να βρείτε τη γωνία των \vec{\alpha}, \vec{\beta}.
  3. Αν \vec{\alpha} = (3, -4) και \vec{\beta} = \dfrac{1}{7}i + j, να βρείτε τη γωνία των \vec{\alpha}, \vec{\beta}.
  4. Αν Α(4, 1), Β(8, 2), Γ(1, 3), να αποδείξετε ότι η γωνία των \overrightarrow{AB}, \overrightarrow{A\Gamma} είναι αμβλεία.

    5. Συνέχεια ανάγνωσης ΑΣΚΗΣΕΙΣ ΕΣΩΤΕΡΙΚΟΥ ΓΙΝΟΜΕΝΟΥ ΜΕΡΟΣ Β. →

Β ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ / ΑΣΚΗΣΕΙΣ ΕΣΩΤΕΡΙΚΟ ΓΙΝΟΜΕΝΟ

ΑΣΚΗΣΕΙΣ ΕΣΩΤΕΡΙΚΟΥ ΓΙΝΟΜΕΝΟΥ ΜΕΡΟΣ Γ.

Σχολιάστε

ΑΣΚΗΣΕΙΣ ΕΣΩΤΕΡΙΚΟΥ ΓΙΝΟΜΕΝΟΥ ΜΕΡΟΣ Γ.

    1. Αν \vec{\alpha}^2 = 5\vec{\beta}(2\vec{\alpha} - 5\vec{\beta}), να αποδείξετε ότι \vec{\alpha}\uparrow \uparrow \vec{\beta}.
    2. Αν το διάνυσμα \vec{\alpha} είναι μοναδιαίο και ισχύει \vec{\beta}^2 + \vec{\gamma}^2 = \vec{\alpha} \cdot (2\vec{\beta} - \vec{\alpha}), να υπολογίσετε την παράσταση Α = \vec{\alpha} \cdot \vec{\beta} + \vec{\beta} \cdot \vec{\gamma}.
    3. Αν το διάνυσμα \vec{\alpha} είναι μοναδιαίο και ισχύει |\vec{\beta}| = 2\sqrt{\vec{\alpha} \cdot \vec{\beta} - 1}, να αποδείξετε ότι \vec{\beta} = 2\vec{\alpha}.
    4.  Αν |\vec{\alpha}| = 2 και |\vec{\beta}| = \sqrt{\vec{\alpha} \cdot \vec{\beta} - 1}, να δείξετε ότι \vec{\alpha} = 2\vec{\beta}.
    5.  Αν τα διανύσματα \vec{\alpha}, \vec{\beta}, \vec{\gamma} είναι μοναδιαία και ισχύει \vec{\alpha} \cdot \vec{\beta} + \vec{\beta} \cdot \vec{\gamma} = 2, να αποδείξετε ότι \vec{\alpha} = \vec{\beta} = \vec{\gamma}.
    6. Αν \vec{\alpha}, \vec{\beta}, \vec{\nu} = \dfrac{|\vec{\beta}|}{|\vec{\alpha}|} \cdot \vec{\alpha} και \vec{\upsilon} = \dfrac{|\vec{\alpha}|}{|\vec{\beta}|} \cdot \vec{\beta}, να αποδείξετε ότι:i.).  \vec{\nu} \uparrow \uparrow \vec{\alpha} και |\vec{\upsilon}| = |\vec{\alpha}|.
      ii.). |\vec{\nu} + \vec{\upsilon}| = |\vec{\alpha} + \vec{\beta}|.
    7.  Αν για τα διανύσματα \vec{\alpha}, \vec{\beta} ισχύουν |\vec{\alpha}| = 2|\vec{\beta}|, ~\vec{\alpha}\neq \vec{0} και |\vec{\alpha} + \vec{\beta}| = |\vec{\beta}|, να αποδείξετε ότι \vec{\alpha} \uparrow\downarrow \vec{\beta}.
    8.  Αν |\vec{\alpha}| = |\vec{\beta}| = |\vec{\alpha} + \vec{\beta}|, να δείξετε ότι |\vec{\alpha} - \vec{\beta}| = |\vec{\alpha}|\sqrt{3}.
    9.  Αν |\vec{\alpha}| = 6 και |\vec{\beta}| = 2 και |\vec{\alpha} + \vec{\beta}| \geq 8, να αποδείξετε ότι:i.). |\vec{\alpha} + \vec{\beta}| = 8.
      ii.).\vec{\alpha} = 3\vec{\beta}.

      ΑΣΚΗΣΕΙΣ ΕΣΩΤΕΡΙΚΟΥ ΓΙΝΟΜΕΝΟΥ ΜΕΡΟΣ Γ.

      10. Συνέχεια ανάγνωσης ΑΣΚΗΣΕΙΣ ΕΣΩΤΕΡΙΚΟΥ ΓΙΝΟΜΕΝΟΥ ΜΕΡΟΣ Γ. →