Επίλυση της εξίσωσης ![]() στην περίπτωση που η
στην περίπτωση που η ![]() είναι γνησίως αύξουσα συνάρτηση.
είναι γνησίως αύξουσα συνάρτηση.
Ισχύει ότι:
![]()
![]()
Παράδειγμα
Δίνεται η συνάρτηση ![]() η οποία είναι γνησίως αυξουσα. Να αποδειχθεί ότι
η οποία είναι γνησίως αυξουσα. Να αποδειχθεί ότι
![]()
Λύση
Θα αποδείξουμε πρώτα ότι από ![]()
Έστω ότι το ![]() είναι ρίζα της
είναι ρίζα της ![]() τότε
τότε ![]()
Άρα
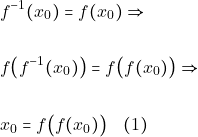
Ας υποθέσουμε τωρα ότι το ![]() δεν είναι ρίζα της εξίσωσης
δεν είναι ρίζα της εξίσωσης ![]() οπότε αφου
οπότε αφου ![]() τότε θα ισχύει
τότε θα ισχύει ![]() ή
ή ![]()
Περίπτωση 1.
Έστω ![]() τότε αφού η
τότε αφού η ![]() είναι γνησίως αύξουσα έχουμε:
είναι γνησίως αύξουσα έχουμε:
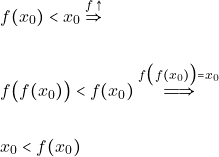
άτοπο αφού αρχικά υποθέσαμε ![]()
Περίπτωση 2.
Έστω ![]() τότε αφού η
τότε αφού η ![]() είναι γνησίως αύξουσα έχουμε:
είναι γνησίως αύξουσα έχουμε:
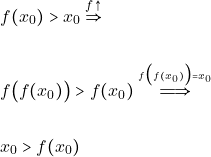
άτοπο αφού αρχικά υποθέσαμε ![]()
Τελικά απο περίπτωση 1 και 2 έχουμε ότι δεν μπορεί να ισχύει ![]() ή
ή ![]() τότε
τότε ![]()
Συνεπώς αν το ![]() είναι ρίζα της
είναι ρίζα της ![]() τότε ειναι και της
τότε ειναι και της ![]() δηλαδή, για κάθε γνησίως αύξουσα συναρτηση
δηλαδή, για κάθε γνησίως αύξουσα συναρτηση ![]() ισχύει η συνεπαγωγή:
ισχύει η συνεπαγωγή:
![]()
Θα αποδείξουμε τώρα το αντίστροφο.
Δηλαδη αν ![]() τότε
τότε ![]()
Έστω ότι το ![]() είναι ρίζα της εξίσωσης
είναι ρίζα της εξίσωσης ![]() τότε
τότε
![]()
δηλαδή έχουμε :
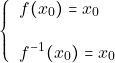
οπότε και ![]()
Συνεπώς αν το ![]() είναι ρίζα της
είναι ρίζα της ![]() τότε ειναι και της
τότε ειναι και της ![]() δηλαδή, για κάθε γνησίως αύξουσα συναρτηση
δηλαδή, για κάθε γνησίως αύξουσα συναρτηση ![]() ισχύει η συνεπαγωγή:
ισχύει η συνεπαγωγή:
![]()
Τελικα για κάθε γνησιως αυξουσα συνάρτηση ισχύει η ισοδυναμία
![]()
Γενικότερα, έστω ![]() μια 1-1 συνάρτηση οπότε ορίζεται η αντίστροφη
μια 1-1 συνάρτηση οπότε ορίζεται η αντίστροφη ![]() Αποδείξαμε ότι αν η
Αποδείξαμε ότι αν η ![]() είναι γνησίως αύξουσα, τότε οι εξισώσεις
είναι γνησίως αύξουσα, τότε οι εξισώσεις ![]() και
και ![]() είναι ισοδύναμες, δηλαδή:
είναι ισοδύναμες, δηλαδή:
![]()
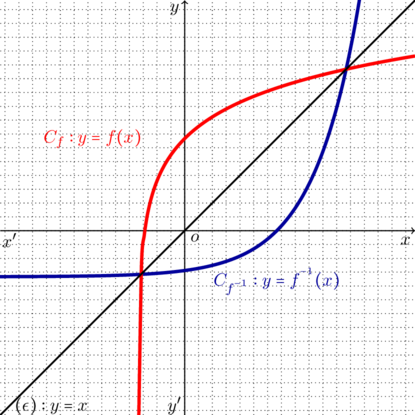
Από τα παραπάνω προκύπτει ότι τα σημεία τομής των γραφικών παραστάσεων ![]() και
και ![]() , είναι τα ίδια με τα σημεία τομής της
, είναι τα ίδια με τα σημεία τομής της ![]() με την
με την ![]() ή της
ή της ![]() με την
με την ![]()
Αν η ![]() δεν είναι γνησίως αύξουσα, τότε οι εξισώσεις
δεν είναι γνησίως αύξουσα, τότε οι εξισώσεις ![]() και
και ![]() δεν είναι ισοδύναμες. Μπορεί δηλαδή να υπάρχουν σημεία τομής των
δεν είναι ισοδύναμες. Μπορεί δηλαδή να υπάρχουν σημεία τομής των ![]() και
και ![]() που δεν ανήκουν στην ευθεία
που δεν ανήκουν στην ευθεία ![]()
Για παράδειγμα η συνάρτηση ![]() έχει πεδίο ορισμού το
έχει πεδίο ορισμού το ![]() και είναι γνησίως φθίνουσα στα διαστήματα
και είναι γνησίως φθίνουσα στα διαστήματα
![]() και
και ![]() Αρα σε κάθε ένα απο αυτα τα διαστήματα είναι και 1-1 συνάρτηση οπότε ορίζεται και η αντίστροφος. Έυκολα βρίσκουμε ότι
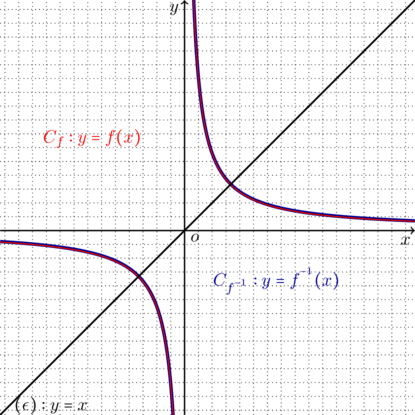
Αρα σε κάθε ένα απο αυτα τα διαστήματα είναι και 1-1 συνάρτηση οπότε ορίζεται και η αντίστροφος. Έυκολα βρίσκουμε ότι ![]() Απο την παρακάτω γραφική απεικόνιση βλέπουμε ότι υπάρχουν σημεία τομής των
Απο την παρακάτω γραφική απεικόνιση βλέπουμε ότι υπάρχουν σημεία τομής των ![]() και
και ![]() που δεν ανήκουν στην ευθεία
που δεν ανήκουν στην ευθεία ![]()
Παράδειγμα
Δίνεται η συνάρτηση ![]()
i) Να αποδείξετε ότι η ![]() είναι αντιστρέψιμη.
είναι αντιστρέψιμη.
ii) Να βρείτε τα σημεία τομής των γραφικών παραστάσεων των ![]() και
και ![]()
Λύση
i)Το πεδίο ορισμού της ![]() είναι το
είναι το ![]() Θα μελετήσουμε την
Θα μελετήσουμε την ![]() ως προς τη μονοτονία.
ως προς τη μονοτονία.
Έστω ![]() με
με ![]()
Έχουμε:
![]()
Προσθέτοντας, κατά μέλη στην ![]() την σχέση
την σχέση ![]() έχουμε:
έχουμε:
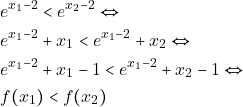
Άρα η ![]() είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο ![]() οπότε είναι 1-1, δηλαδή αντιστρέψιμη.
οπότε είναι 1-1, δηλαδή αντιστρέψιμη.
ii) Η ![]() με
με ![]() τέμνει την
τέμνει την ![]() με
με ![]() όταν
όταν
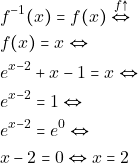
Αφου η ![]() είναι γνησίως αύξουσα συνάρτηση στο
είναι γνησίως αύξουσα συνάρτηση στο ![]() τότε η
τότε η ![]() και
και ![]() τέμνονται πάνω στην ευθεία
τέμνονται πάνω στην ευθεία ![]() οπότε για
οπότε για ![]() το σημείο τομής είναι το
το σημείο τομής είναι το ![]()
Βιβλιογραφία: Παπαδάκης, εκδόσεις Σαββάλα. Δ.Α.Παπακωνσταντίνου, αυτοέκδοση.
Λουκόπουλος εκδόσεις Εν Δυνάμει.

Αυτή η εργασία χορηγείται με άδεια Creative Commons Αναφορά Δημιουργού – Μη Εμπορική Χρήση – Παρόμοια Διανομή 4.0 Διεθνές .
