Γ Λυκείου,ΟΡΙΟ ΣΥΝΑΡΤΗΣΗΣ ΣΤΟΥΣ ΠΡΑΓΜΑΤΙΚΟΥΣ ΑΡΙΘΜΟΥΣ

ΥΠΟΛΟΓΙΣΜΟΣ ΟΡΙΟΥ

Σχολιάστε
Print Friendly, PDF & Email

Για τον υπολογισμο του ορίου μιας συνάρτησης f στο x_{0}, ισχύουν ότι:

ΓΕΝΙΚΑ.

    \[\displaystyle\lim_{x\to x_{0}} x = x_{0}.\]

    \[\displaystyle\lim_{x\to x_{0}}c =c.\]

ΒΑΣΙΚΕΣ ΙΔΙΟΤΗΤΕΣ ΤΟΥ ΟΡΙΟΥ.

* \displaystyle\lim_{x\to x_{0}}f(x) = l \Leftrightarrow \displaystyle\lim_{x\to x_{0}}[f(x) -l] =0.

* \displaystyle\lim_{x\to x_{0}}f(x) = l \Leftrightarrow \displaystyle\lim_{h\to 0}f(x_{0}+h) =l.

* \displaystyle\lim_{x\to x_{0}}f(x) = 0 \Leftrightarrow \displaystyle\lim_{x\to x_{0}}|f(x)| = 0.

* \displaystyle\lim_{x\to x_{0}}f(x) = l \Leftrightarrow \displaystyle\lim_{x\to x_{0}}\big[-f(x)\big] =-l.

ΟΡΙΑ ΚΑΙ ΠΡΑΞΕΙΣ.
Ο υπολογισμός ενός ορίου πραγματοποιείται συνήθως με τη βοήθεια των παρακάτω ιδιοτήτων, που ισχύουν
ΜΟΝΟ στην περίπτωση που τo \displaystyle\lim_{x\to x_{0}}f(x) και το \displaystyle\lim_{x\to x_{0}}g(x) ΥΠΑΡΧΟΥΝ.

* \displaystyle\lim_{x\to x_{0}}\Big(f(x)+g(x)\Big) =\displaystyle\lim_{x\to x_{0}}f(x) +\displaystyle\lim_{x\to x_{0}}g(x).

* \displaystyle\lim_{x\to x_{0}}\Big(f(x)\cdot g(x)\Big) = \displaystyle\lim_{x\to x_{0}}f(x) \cdot \displaystyle\lim_{x\to x_{0}}g(x).

* \displaystyle\lim_{x\to x_{0}}\dfrac{f(x)}{g(x)} = \dfrac{\displaystyle\lim_{x\to x_{0}}f(x)}{\displaystyle\lim_{x\to x_{0}}g(x)}, εφόσον \displaystyle\lim_{x\to x_{0}}g(x)\neq 0.

* \displaystyle\lim_{x\to x_{0}}\Big|f(x)\Big| = \bigg|\displaystyle\lim_{x\to x_{0}}f(x)\bigg|.

* \displaystyle\lim_{x\to x_{0}}\sqrt[\nu]{f(x)} = \sqrt[\nu]{\displaystyle\lim_{x\to x_{0}}f(x)}, εφόσον f(x)\geq 0 κοντά στο x_{0}.

* \displaystyle\lim_{x\to x_{0}}f^{\nu}(x) = \bigg[ \displaystyle\lim_{x\to x_{0}}f(x)\bigg]^{\nu}.

* \displaystyle\lim_{x\to x_{0}}\big(\lambda \cdot f(x) \big) = \lambda \cdot \displaystyle\lim_{x\to x_{0}}f(x) με \lambda \in \mathbb{R}.

Για τον υπολογισμό ενός ορίου \displaystyle\lim_{x \to x_{o}}f(x) βρίσκουμε πρώτα, το πεδίο ορισμού της f, προκειμένου να ελέγξουμε αν έχει νόημα η αναζήτηση του ορίου. Στη συνέχεια, για να υπολογίσουμε το \displaystyle\lim_{x \to x_{o}}f(x), θέτουμε όπου x το x_{o} και εφόσον το αποτέλεσμα είναι ένας πραγματικός αριθμός l \in \mathbb{R} (δηλαδη, δεν προκύπτουν απροσδιόριστες μορφές,) τότε το όριο είναι ίσο με l.

Παράδειγμα.1
Να υπολογιστούν τα παρακάτω όρια:
i ) \displaystyle\lim_{x\to 3} \sqrt{x+6}.

ii ) \displaystyle\lim_{x\to 3}(x^{3} -2x +3).

iii) \displaystyle\lim_{x\to 3}| 2x+1|.

Λύση

i ) Θεωρούμε τη συνάρτηση f(x)= \sqrt{x+6} για την οποία θα πρέπει x+6\geq 0 \Leftrightarrow x\geq -6.
Άρα το πεδίο ορισμού είναι A_{f}=[-6,+\infty)
και άρα το \displaystyle\lim_{x\to 3}f(x) ορίζεται.
Συνεπώς \displaystyle\lim_{x\to 3}\sqrt{x+6} = \sqrt{3+6} =\sqrt{9}=3.
Δηλαδή \displaystyle\lim_{x\to 3}\sqrt{x+6} =3.

ii ) Θεωρούμε τη συνάρτηση g(x) = x^{3} -2x +3, η οποία έχει πεδίο ορισμού A_{g}= \mathbb{R}.
Άρα το \displaystyle\lim_{x\to 3}g(x) ορίζεται.
Συνεπώς:

    \begin{align*} \displaystyle\lim_{x\to 3}g(x)=\displaystyle\lim_{x\to 3}(&x^{3} -2x +3)=\\ &3^{3} -2\cdot 3 +3 =\\ &27-6 +3=24. \end{align*}

Δηλαδή \displaystyle\lim_{x\to 3}(x^{3} -2x +3)=24.

iii ) Ομοίως έχουμε ότι

\displaystyle\lim_{x\to 3}(2x+1) = 2\cdot 3 +1=6+1=7.

Οπότε το

\displaystyle\lim_{x\to 3}|2x+1|=\big| \displaystyle\lim_{x\to 3}(2x+1)\big|=|7|=7.

Παράδειγμα.2
Να υπολογίσετε το όριο

    \[\lim_{x \to 3}\dfrac{\sqrt{x+6}-x^3+2x-3}{|2x+1|-5}\]

Λύση
Έχουμε

    \begin{align*} &\lim_{x \to 3}\dfrac{\sqrt{x+6}-x^3+2x-3}{|2x+1|-5}=\\\\ &\lim_{x \to 3}\dfrac{\sqrt{x+6}-(x^3-2x+3)}{|2x+1|-5}. \end{align*}

Θεωρούμε τη συνάρτηση f(x) = \dfrac{\sqrt{x+6}-(x^3-2x+3)}{|2x+1|-5}.
για την οποία θα πρέπει

    \[x+6\geq 0 \Leftrightarrow x\geq -6\]

και

    \begin{align*} &|2x+1|-5\neq 0\Leftrightarrow\\ &|2x+1|\neq 5\Leftrightarrow \\\\ & \left\{ \begin{tabular}{ll} $2x+1\neq 5,$ \\\\ $2x+1\neq -5$ \end{tabular} \right.\Leftrightarrow \\\\ & \left\{ \begin{tabular}{ll} $2x\neq 5-1,$ \\\\ $2x\neq -5-1$ \end{tabular} \right.\Leftrightarrow \\\\ & \left\{ \begin{tabular}{ll} $2x\neq 4,$ \\\\ $2x\neq -6$ \end{tabular} \right.\Leftrightarrow \\\\ & \left\{ \begin{tabular}{ll} $x\neq 2,$ \\\\ $x\neq -3$ \end{tabular} \right. \end{align*}

Για να βρούμε το πεδιο ορισμού της συνάρτησης f, συναληθεύουμε τους παραπάνω περιορισμούς:

Rendered by QuickLaTeX.com

και έχουμε ότι:

    \[A_{f}=[-6,-3)\cup (-3,2)\cup (2,+\infty)\]

Άρα το \displaystyle\lim_{x\to 3}f(x) έχει νόημα.

Επιλέον στο Παράδειγμα.1 δείξαμε οτι υπάρχουν, αλλα και υπολογίσαμε τα όρια

    \[\displaystyle\lim_{x\to 3}\sqrt{x+6} =3.\]

    \[\displaystyle\lim_{x\to 3}(x^{3} -2x +3)=24.\]

    \[\displaystyle\lim_{x\to 3}|2x+1|=7.\]

Τελικά το ζητούμενο όριο γίνεται:

    \begin{align*} &\lim_{x \to 3}\dfrac{\sqrt{x+6}-x^3+2x-3}{|2x+1|-5}=\\\\ &\lim_{x \to 3}\dfrac{\sqrt{x+6}-(x^3-2x+3)}{|2x+1|-5}\\\\ &\dfrac{\displaystyle\lim_{x \to 3}\sqrt{x+6}-\displaystyle\lim_{x \to 3}(x^3-2x+3)}{\displaystyle\lim_{x \to 3}\big(|2x+1|\big)-5}\\\\ &\dfrac{3-24}{7-5}= \dfrac{-21}{2} \end{align*}

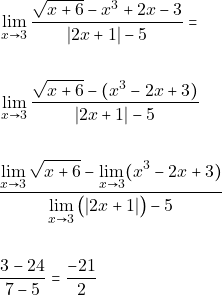
Παράδειγμα.3
Αν υπάρχουν τα όρια \displaystyle\lim_{x\to x_{0}}\big(f(x) +g(x)\big)\in \mathbb{R} και \displaystyle\lim_{x\to x_{0}}g(x)\in \mathbb{R}, να δειχθεί ότι υπάρχει στο \mathbb{R} το \displaystyle\lim_{x\to x_{0}}f(x).

Λύση

Επειδή υπάρχουν στο \mathbb{R} τα όρια, υποθέτουμε ότι \displaystyle\lim_{x\to x_{0}}\big(f(x) +g(x)\big)=m και \displaystyle\lim_{x\to x_{0}}g(x)=l
επίσης για την f ισχύει

    \[f(x) = \big(f(x)+g(x)\big)-g(x)\]

Έχουμε ότι:

    \begin{align*} \displaystyle\lim_{x\to x_{0}}f(x)= &\displaystyle\lim_{x\to x_{0}}\Bigg(\big(f(x)+g(x)\big)-g(x)\Bigg) \\\\ = &\displaystyle\lim_{x\to x_{0}}\big(f(x)+g(x)\big)-\displaystyle\lim_{x\to x_{0}}g(x)\\\\ = &m-l. \end{align*}

Τελικά το \displaystyle\lim_{x\to x_{0}}f(x) υπάρχει και είναι πραγματικός αριθμός.

Βιβλιογραφία: Παπαδάκης, εκδόσεις Σαββάλα, Στεργίου, Νακής, εκδόσεις Σαββάλα, Παπακωνσταντίνου, αυτοέκδοση.
Άδεια Creative Commons
Αυτή η εργασία χορηγείται με άδεια Creative Commons Αναφορά Δημιουργού – Μη Εμπορική Χρήση – Παρόμοια Διανομή 4.0 Διεθνές .

Αφήστε μια απάντηση

Η ηλ. διεύθυνση σας δεν δημοσιεύεται. Τα υποχρεωτικά πεδία σημειώνονται με *

Δεν είμαι Robot *